Referendum w sprawie obliczeń wielopodmiotowych
26.12.2010 - Agata Murawska
    A co z referendum?Można stwierdzić, że skoro zliczanie sumy jedynek da się sprowadzić do stworzenia obwodu logicznego, to problem jest rozwiązany. Z drugiej strony wydaje się, że powyższa metoda, jakkolwiek dość ogólna, ma jedną poważną wadę - jest POTWORNIE wolna! Może da się zatem podejść do sprawy nieco mniej ogólnie i wymyślić prostą metodę, która zdąży obliczyć wynik przed następnymi wyborami?
Przypomnijmy dane do zadania:
Niech
Wybiera się (w dowolny sposób) liczbę Wskazówka Czy to aby bezpieczne?Można zastanawiać się dalej - na ile wiarygodne są obliczone przez nas wartości? Jaki poziom bezpieczeństwa jesteśmy w stanie zapewnić, jeśli wiemy, że część użytkowników systemu jest w zmowie i udostępnia sobie na wzajem poznane informacje? Ilu z nich może współpracować bez zakłócenia pracy systemu, jeśli oszukują i działają niezgodnie z protokołem? Nie wchodząc w matematyczne szczegóły powiemy tylko, że umiemy projektować protokoły, które pozostają bezpieczne nawet, jeśli połowa użytkowników jest w zmowie i przekazuje sobie wszystke dane (prywatne, jak i uzyskane za pośrednicwem protokołu).
Przy zapewnianiu bezpieczeństwa mając do czynienia z tak zwanymi przeciwnikami aktywnymi, czyli nie działającymi według zasad protokołu radzimy sobie, póki jest ich mniej, niż Dokąd to wszystko zmierza?Jak łatwo się domyślić na podstawie powyższego protokołu, w tej chwili rozważania dotyczące obliczeń wielopodmiotowych koncentrują się raczej na szukaniu wydajnych i bezpiecznych rozwiązań znanych problemów, niż wynajdywaniu kolejnych metod uniwersalnych. W tym wypadku stwierdzenie “kiedy coś jest do wszystkiego, to jest do niczego” sprawdza się niemal bezbłędnie. Zadania sprawdzające
Artykuł powstał częściowo na podstawie notatek doktora Stefana Dziembowskiego do wykładów na Uniwersytecie Warszawskim oraz University of Rome - La Sapienza.
Obrazki bramek logicznych i sumatora dwubitowego pochodzą z wikipedii. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 osób, wyrażających swoją opinię na dany temat. Zostaje im zadanie jedno pytanie, na które mogą odpowiedzieć “tak” (co odpowiada wartości
osób, wyrażających swoją opinię na dany temat. Zostaje im zadanie jedno pytanie, na które mogą odpowiedzieć “tak” (co odpowiada wartości  ) albo “nie” (
) albo “nie” ( ). Naszym zadaniem jest obliczenie, ile było głosów “za” - a zatem sumy pewnej liczby jedynek.
). Naszym zadaniem jest obliczenie, ile było głosów “za” - a zatem sumy pewnej liczby jedynek.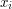 oznacza głos
oznacza głos  -tego uczestnika protokołu. Chcemy zatem obliczyć
-tego uczestnika protokołu. Chcemy zatem obliczyć 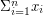 . Jak?
. Jak?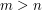 .
.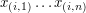 w taki sposób, że
w taki sposób, że 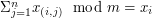 , a następnie rozsyła fragmenty do wszystkich w taki sposób, że osoba
, a następnie rozsyła fragmenty do wszystkich w taki sposób, że osoba  dostaje od osoby
dostaje od osoby 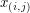 .
.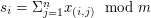
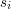 zostają upublicznione - przesłane wspólnym kanałem rozgłoszeniowym. Aby poznać wynik referendum pozostaje obliczyć
zostają upublicznione - przesłane wspólnym kanałem rozgłoszeniowym. Aby poznać wynik referendum pozostaje obliczyć 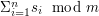
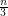 .
.


