Własny silnik graficzny. Część IV: krwawienie kolorów i miękkie cienie.
30.11.2010 - Robert Kraus
    Całkowanie w naszym kodzie
Procedura
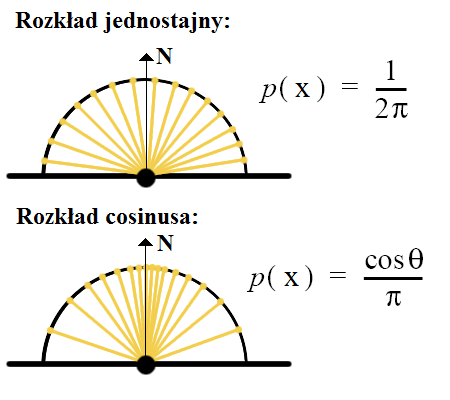
We wzorze na gęstość w rozkładzie cosinusa
Wróćmy teraz do procedury
Tak wygląda całka w przypadku naszego zagadnienia oświetlenia:
1) 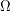 to zbiór wszystkich kierunków na półsferze to zbiór wszystkich kierunków na półsferze 2)  dowolny kierunek z półsfery dowolny kierunek z półsfery 3) 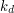 jest to kolor powierzchni (współczynnik odbicia rozproszonego materiału) jest to kolor powierzchni (współczynnik odbicia rozproszonego materiału) 4) 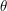 to kąt pomiędzy kierunkiem na półsferze a wektorem normalnym do powierzchni to kąt pomiędzy kierunkiem na półsferze a wektorem normalnym do powierzchni 5) 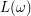 ilość światła docierająca do trafionego punktu z kierunku ilość światła docierająca do trafionego punktu z kierunku  Nasza całkowana funkcja ma postać:
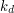 w naszym kodzie to w naszym kodzie to 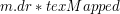 , , a 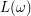 to to 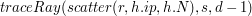 . .
Pamiętamy jednak, że prosty estymator Podsumowanie Nauczyliśmy się jak przy pomocy śledzenia promieni generować zdjęcia wirtualnej sceny. Poznaliśmy zjawiska takie jak odbicia zwierciadlane, odbicia rozproszone, transmisja z refrakcją, miękke cienie, krwawienie kolorów. Dowiedzieliśmy się jak teksturować powierzchnie obiektów. Niedługo pojawią się kolejne części tego cyklu artykułów, w których scalimy wszystkie dotychczas poznane zjawiska tworząc program obsługujący ścieżki typów E (D|S|T)* L. Poznamy zjawisko kaustyk. Dodamy do kamery symulację systemu optycznego, który pozwoli uzyskać efekt głębi ostrości. Dowiemy się trochę więcej o symulacji lokalnych zjawisk związanych z odbijaniem światła. Na sam koniec wprowadzimy obsługę siatek trójkątów i bardziej skomplikowanej geometrii, żeby zobaczyć coś ciekawszego od kilku kulek :) Część I Część II Część III Część IV
(4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


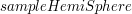 daje w wyniku losowy kierunek z półsfery
losując kierunki z rozkładem cosinusa. Poniżej ilustracja pokazująca
różnicę pomiędzy rozkładem jednostajnym i cosinusa. W rozkładzie jednostajnym
kierunki podczas losowania rozkładają się równomiernie po półsferze,
natomiast w rozkładzie cosinusa kierunki bedą występować gęściej wokół wektora normalnego
do powierzchni, na której leży punkt, w którym obliczamy oświetlenie.
daje w wyniku losowy kierunek z półsfery
losując kierunki z rozkładem cosinusa. Poniżej ilustracja pokazująca
różnicę pomiędzy rozkładem jednostajnym i cosinusa. W rozkładzie jednostajnym
kierunki podczas losowania rozkładają się równomiernie po półsferze,
natomiast w rozkładzie cosinusa kierunki bedą występować gęściej wokół wektora normalnego
do powierzchni, na której leży punkt, w którym obliczamy oświetlenie.
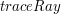 .
.
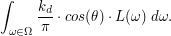
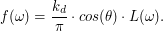
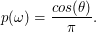
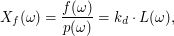
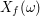 był mało zadowalający.
Radziliśmy sobie używając wielu prób prostego estymatora, obliczając średnią arytmetyczną uzyskanych wyników.
Ten lepszy estymator realizowany jest przez funkcję
był mało zadowalający.
Radziliśmy sobie używając wielu prób prostego estymatora, obliczając średnią arytmetyczną uzyskanych wyników.
Ten lepszy estymator realizowany jest przez funkcję 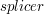 , która wcześniej służyła jedynie do realizacji antyaliasingu.
, która wcześniej służyła jedynie do realizacji antyaliasingu.


