Własny silnik graficzny. Część IV: krwawienie kolorów i miękkie cienie.
30.11.2010 - Robert Kraus
    Pod niewielkimi zmianami w kodzie kryje się trochę matematyki. Dowiemy się teraz dlaczego to, co zrobiliśmy, działa. Całkowanie
Niespodzianka, a teraz nauczymy się całkować.
Interesować nas będzie geometryczna interpretacja całki, która mówi, że Przykład 1
Niech
Przykład 2
Niech
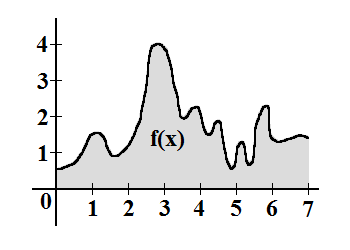
Przykład 3 Niech teraz funkcja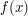 , będzie taka jak na poniższej ilustracji. W przypadku takiej funkcji pojawia
się problem ("gołym okiem" niezbyt widać ile wynosi pole pod wykresem takiej funkcji).
Teraz poradzimy sobie całkowaniem stochastycznym. , będzie taka jak na poniższej ilustracji. W przypadku takiej funkcji pojawia
się problem ("gołym okiem" niezbyt widać ile wynosi pole pod wykresem takiej funkcji).
Teraz poradzimy sobie całkowaniem stochastycznym.
Całkowanie stochastyczne Całkowanie stochastyczne polega na oszacowaniu (przybliżeniu) wartości całki w sposób losowy. Konstruujemy coś, co będzie przybliżało wartość interesującej nas całki (będzięmy to nazywać estymatorem). Estymator zdefiniowany jest następująco:
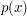 jest gęstością rozkładu z jaką wylosowano próbkę jest gęstością rozkładu z jaką wylosowano próbkę  z dziedziny funkcji z dziedziny funkcji 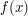 . .
Na początek oswoimy się z pojęciem rozkładu. Intuicyjnie rozkład warunkuje to, w których miejscach dziedziny funkcji punkty będą losowane z większym prawdopodobieństwem, a w których z mniejszym (co skutkuje tym, że jak wylosujemy przykładowo 100 punktów, to w jednych obszarach dziedziny mogą powstawać gęstsze skupiska punktów, a w innych punkty będą występować sporadycznie).
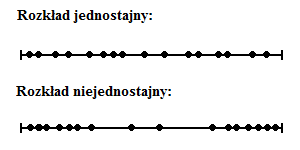
Na powyższej ilustracji widać przykład dwóch rozkładów. Wylosowano 16 punktów na odcinku. W rozkładzie jednostajnym punkty rozkładają się na odcinku równomiernie (tj. nie mają wyraźnej tendencji do grupowania się tylko w pewnych miejscach). Natomiast w rozkładzie niejednostajnym punkty mogą sie grupować tak jak na ilustracji na końcach odcinka oraz rzadko występować w okolicy jego środka.
Skupimy sie teraz na rozkładzie jednostajnym. Z rozkładem związane jest pojęcie
gęstości. Detale teoretyczne takie jak wyprowadzanie gęstości dla konkretnego
rozkładu oraz czym dokładnie jest gęstość wybiegają nieco poza poziom trudności tego artykułu,
więc funkcje gęstości dla rozkładów bedą podawane jako fakty, w które należy uwierzyć bez dowodu.
Dla rozkładu jednostajnego funkcja gęstości jest równa odwrotności długości odcinka, bądź polu lub objętości zbioru,
z którego losujemy punkty.
Przykładowo dla odcinka długości 10 funkcja gęstości to
Przekonajmy się, że to wszystko rzeczywiście działa. Wrócmy do przykładu nr 1 całkowania.
Mamy funkcję
![$ [a,b] $](/files/tex/9954daf8330e5a19f1c7b4b890ccec79f8afce2c.png) , to
dla rozkładu jednostajnego na tym odcinku funkcja gęstości wynosi , to
dla rozkładu jednostajnego na tym odcinku funkcja gęstości wynosi  .
Zgodnie z definicją estymator dla funkcji .
Zgodnie z definicją estymator dla funkcji 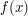 to to
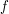 jest zawsze jest zawsze 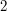 , to: , to:
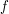 na odcinku na odcinku ![$ [a,b] $](/files/tex/9954daf8330e5a19f1c7b4b890ccec79f8afce2c.png) . .
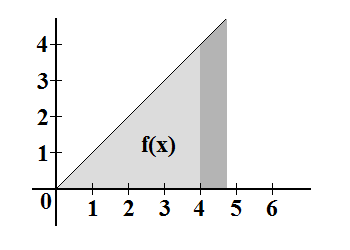
Sprawdźmy teraz co się dzie w przypadku przykładu nr 2 całkowania.
Mamy funkcję
![$ [0,4] $](/files/tex/f359b03b12d86c902037ae42ce3e2cb112efeceb.png) , to dla rozkładu jednostajnego
na tym odcinku funkcja gęstości wynosi , to dla rozkładu jednostajnego
na tym odcinku funkcja gęstości wynosi 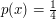 .
Zgodnie zdefinicją estymator dla funkcji .
Zgodnie zdefinicją estymator dla funkcji 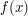 to to
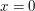 , to , to 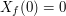 , a jeśli wylosujemy , a jeśli wylosujemy 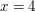 , to , to 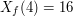 .
Widzimy zatem, że nasz prosty estymator bardzo słabo przybliża wartość naszej całki.
Teraz zrobimy użytek naszego rozkładu i skonstruujemy lepszy estymator.
Niech .
Widzimy zatem, że nasz prosty estymator bardzo słabo przybliża wartość naszej całki.
Teraz zrobimy użytek naszego rozkładu i skonstruujemy lepszy estymator.
Niech 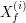 oznacza wartość estymatora w oznacza wartość estymatora w 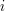 -tej próbie
(tj. wiele razy losujemy -tej próbie
(tj. wiele razy losujemy  i obliczamy i obliczamy 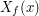 dla każdego losowania),
a dla każdego losowania),
a ![$ X_f^{[n]} $](/files/tex/7c1800ef549847e8acb29e6bcbe0d4fcf991d1b1.png) niech oznacza średnią arytmetyczną wartości niech oznacza średnią arytmetyczną wartości 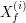 , czyli: , czyli:
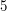 elementów z dziedziny funkcji elementów z dziedziny funkcji 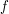 .
Skoro losujemy z rozkładem jednostajnym możliwa jest sytuacja,
w ktorej wylosujemy punkty .
Skoro losujemy z rozkładem jednostajnym możliwa jest sytuacja,
w ktorej wylosujemy punkty 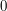 , , 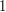 , , 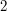 , , 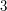 , ,  . Dla każdego wylosowanego
punktu obliczamy . Dla każdego wylosowanego
punktu obliczamy 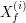 : :
![$ X_f^{[5]} $](/files/tex/4fedc855554ea4d8036eedfbe6bf0d46be1aa077.png) : :
(4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


![$ \int \limits_{x \in [a,b]} f(x) dx $](/files/tex/d094c95306c383ca437bc2f9d4ebf3063e94844e.png) (czyt. całka z funkcji
(czyt. całka z funkcji 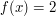 . Zauważmy, że na odcinku
. Zauważmy, że na odcinku ![$ [a, b] $](/files/tex/8b7e5374c801ee7800a3f40ca54e463c8d65a895.png) pole pod wykresem funkcji
pole pod wykresem funkcji 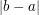 . A więc:
. A więc:
![$$ \int \limits_{x \in [a,b]} f(x) dx = 2 \cdot |b-a| $$](/files/tex/af6c1de123b8831065989034c2923f0a28c0fe4c.png)
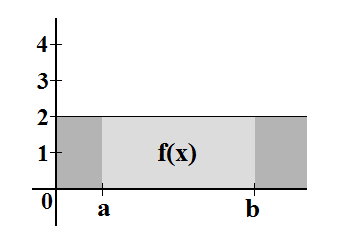
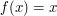 . Zauważmy, że na odcinku
. Zauważmy, że na odcinku ![$ [0, 4] $](/files/tex/f221136d176e76bb9cae70b7297f177e563a0848.png) pole pod wykresem funkcji
pole pod wykresem funkcji ![$$ \int \limits_{x \in [0,4]} f(x) dx = \frac{4 \cdot 4}{2} = 8 $$](/files/tex/24de20864959e8b3c6c395e958410852b5aabbf4.png)
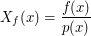
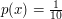 ,
a dla prostokąta o polu 25 funkcja gęstości to
,
a dla prostokąta o polu 25 funkcja gęstości to 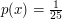 .
.

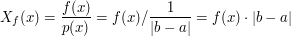
![$$ X_f(x) = 2 \cdot |b-a| = \int \limits_{x \in [a,b]} f(x) dx $$](/files/tex/b4851d21df7efacc707674a7f9afdf545cbb653a.png)
![$$ \int \limits_{x \in [0,4]} f(x) dx = 8 $$](/files/tex/5319dfc75fb01643e7208e5bbb15a981207ad1e0.png)
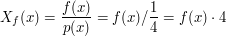
![$$ X_f^{[n]} = \frac{1}{n} \cdot \sum_{i=1}^n X_f^{(i)} = \frac{1}{n} \cdot ( X_f^{(1)} + X_f^{(2)} + ... + X_f^{(n)}) $$](/files/tex/8b9ce8d390502a8620102ab637303091c02de365.png)
![$$ \lim_{n \rightarrow \infty} X_f^{[n]} = \int \limits_{x \in [0,4]} f(x) dx $$](/files/tex/9e4cbd75fe10c86b6c801f9ce21d684a7411dcd3.png)
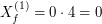
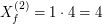
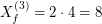
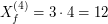
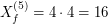
![$$ X_f^{[5]} = \frac{X_f^{(1)}+X_f^{(2)}+X_f^{(3)}+X_f^{(4)}+X_f^{(5)}}{5} $$](/files/tex/60068770da0b7ace1811dde9024a22c8363c5cc1.png)
![$$ X_f^{[5]} = \frac{0+4+8+12+16}{5} = \frac{40}{5} = 8 = \int \limits_{x \in [0,4]} f(x) dx $$](/files/tex/401e193ea1798691ef2ab864dacce9fe2413de51.png)


