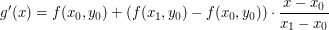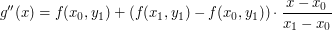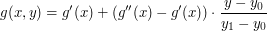Własny silnik graficzny. Część III: teksturowanie.
30.11.2010 - Robert Kraus
    Część I Część II Część III Część IV Czym będziemy się zajmować? Poznamy metody próbkowania i filtrowania (wygładzania) tesktury. Dowiemy się jak teksturować sferę i trójkąt oraz jak uzyskiwać wypukłości na płaskich powierchniach przy pomocy techniki zwanej mapowaniem wektorów normalnych. Wektor 2d
Podstawowe operacje dla
Tekstura Reprezentacja tekstur w kodzie programu:
Teksel (ang. texel) to element tekstury (ang. texture element), podobnie jak piksel to element obrazu (ang. pixel ~ picture element).
Wczytywanie tekstury z pliku jest związane z użyciem bibliotek do wczytywania obrazów,
więc zostaje pominięte. W dołączonym do artykułu programie wczytywanie realizują funkcje
Filtrowanie tekstury
Bbędziemy posługiwali się współrzędnymi Poznamy dwie metody radzenia sobie z tym problemem - próbkowanie punktowe oraz filtrowanie dwuliniowe. Poniższa ilustracja prezentuje efekty stosowania tych metod.

Próbkowanie punktowe
O urokach próbkowania punktowego można się przekonać grając w stare gry 3d takie jak Doom czy Quake
lub jeśli to możliwe wyłączając filtrowanie w jakiś nowszych grach.
Zaokrąglamy współrzędne do części całkowitej otrzymując w ten sposób współrzędne konkretnego teksela. To proste rozwiązanie ma jednak bardzo poważną wadę. Jeśli zbliżymy się do obiektu na dostatecznie krótki dystans widoczne bedą jednokolorowe kwadraty. Ponadto tekstura może wyglądać jakby była zrobiona z przypadkowych ziarenek, które co gorsze lekko migotają gdy obiekt lub obserwator jest w ruchu (efekt szczególnie widoczny w przypadku tekstur mających charakter szachownicy).
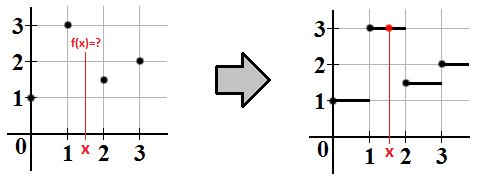
Poniżej implementacja. W wierszach nr 3-4 obliczamy współrzędne teksela zgodnie z powyższym opisem, następnie w wierszu nr 5 obliczamy współrzędne tekstela w tablicy i dzielimy modulo rozmiar tekstury na wypadek wyskoczenia poza rozmiar tekstury (może się to zdarzyć z powodu ograniczonej precyzji liczb w reprezentacji zmiennopozycyjnej).
Filtrowanie dwuliniowe
Pierwsze karty graficzne 3d (zwane akceleratorami, np. voodoo 3dfx)
polegały właśnie na sprzętowej realizacji filtrowania dwuliniowego.
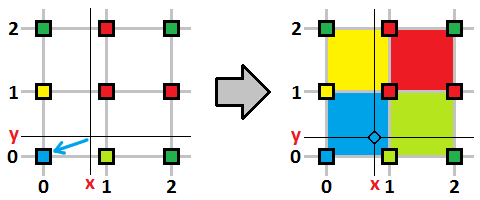
Filtrowanie 2-liniowe (ang. bilinear filtering) polega na zastosowaniu interpolacji dwuliniowej w celu wyznaczenia wartości pośredniej pomiędzy tekstelami. Rozwiązanie to eliminuje efekt ziarenek powodując, że tekstura jest gładka. Natomiast obserwując obiekt z bliskiej odległości zamiast jednokolorowych kwadratów będziemy widzieli rozmyte plamy, co też jest niekoniecznie przyjemne, ale przy teksturze w dostatecznie wysokiej rozdzielczości daje rezultaty lepsze niż próbkowanie punktowe.
A co to jest interpolacja? Rozważmy pewną funkcję
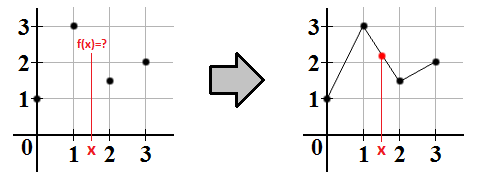
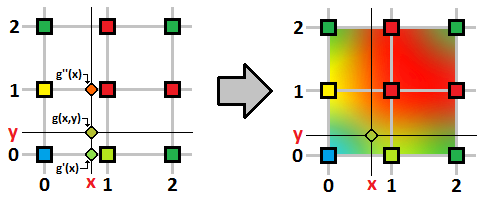
Interpolacja dwuliniowa jest uogólnieniem interpolacji liniowej dla funkcji dwóch zmiennych.
A więc znamy wartości pewnej funkcji
Do powyższych dwóch wartości możemy zastosować interpolację liniową wględem zmiennej  : :
Jak to się ma do naszej tekstury? Jeśli z mapowania na współrzędne tekstury i mnożeniu przez jej rozmiar otrzymamy punkt 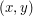 ,
to wartość w tym punkcie obliczamy stosując wyżej omówioną interpolację dwuliniową do punktów ,
to wartość w tym punkcie obliczamy stosując wyżej omówioną interpolację dwuliniową do punktów
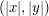 , , 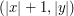 , , 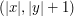 , , 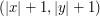 ,
gdzie ,
gdzie 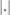 to część całkowita z liczby. to część całkowita z liczby.
Implementacja:
(2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


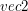 to element przestrzeni dwuwymiarowej, będzie służył
głównie do obliczeń związanych z wyznaczaniem punktów na teksturze.
to element przestrzeni dwuwymiarowej, będzie służył
głównie do obliczeń związanych z wyznaczaniem punktów na teksturze.
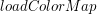 oraz
oraz 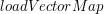 , które można podglądnąć w pełnym kodzie programu.
, które można podglądnąć w pełnym kodzie programu.
![$ (u, v) \in [0,1]^2 $](/files/tex/7d57a462eaf96022a6da740128b4554660a41b31.png) .
Tekstury mają jednak postać krat tekseli o współrzędnych
.
Tekstury mają jednak postać krat tekseli o współrzędnych 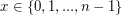 oraz
oraz 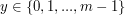 .
Naturalnie należy przeskalować współrzędne z kwadratu
.
Naturalnie należy przeskalować współrzędne z kwadratu ![$ [0,1]^2 $](/files/tex/70fc64cc7adba20f42360409e1448826d452b932.png) na prostokąt
na prostokąt ![$ [0,n-1] \times [0,m-1] $](/files/tex/515b9e01a388a9c21e6905a0b27cf84575b7a362.png) wykonując mnożenie współrzędnych
wykonując mnożenie współrzędnych 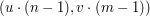 .
Jak łatwo się domyślić, nieczęsto w wyniku takiego przeskalowania otrzymamy współrzędne będące liczbami całkowitymi,
a więc na ogół nie będziemy trafiali w teksele naszej tekstury. Co robić?
.
Jak łatwo się domyślić, nieczęsto w wyniku takiego przeskalowania otrzymamy współrzędne będące liczbami całkowitymi,
a więc na ogół nie będziemy trafiali w teksele naszej tekstury. Co robić?
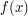 i przypuśćmy,
że znamy jej wartości w punktach
i przypuśćmy,
że znamy jej wartości w punktach 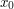 oraz
oraz 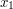 , ale nie znamy wzoru na funkcję
, ale nie znamy wzoru na funkcję 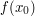 oraz
oraz 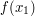 , ale chcielibyśmy umieć też liczyć wartości tej funkcji w punktach
, ale chcielibyśmy umieć też liczyć wartości tej funkcji w punktach 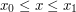 .
.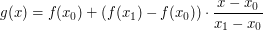
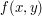 w czterach punktach
w czterach punktach 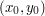 ,
, 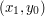 ,
, 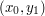 ,
, 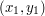 .
Chcemy obliczać
.
Chcemy obliczać 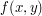 dla
dla 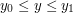 .
Jeśli ustalimy wartość zemiennej
.
Jeśli ustalimy wartość zemiennej  .
Podstawiając za
.
Podstawiając za 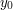 oraz
oraz 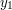 możemy użyć interpolacji liniowej względem zmiennej
możemy użyć interpolacji liniowej względem zmiennej