Własny silnik graficzny. Część III: teksturowanie.
30.11.2010 - Robert Kraus
    Mapowanie wypukłości Istnieje kilka technik mapowania wypukłości, my zajmiemy sie jedną z nich - mapowaniem wektorów normalnych (ang. normal mapping, dot3 bump mapping). Metoda ta polega na zakrzywianiu lub zastępowaniu wektora normalnego w różnych punktach powierzchni obiektu tak, aby uzyskać efekt wgłębień i wypukłości na gładkiej powierzchni. Wykorzystuje się do tego również tekstury w postaci bitmap z tą różnicą, że teksele zawierają teraz inną informację. W każdym tekselu zakodowany jest wektor normalny (czyli wektor prostopadły do powierzchni obiektu). Na poniższym obrazku widać efekt zastosowania metody mapowania wypukłości. W rzeczywistości powierzchnia sfery po prawej stronie jest tak samo gładka jak sfery po lewej stronie, jednak zakrzywione wektory normalne dają złudzenie nierówności... niestety to złudzenie kończy się na brzegu, gdzie nasza sfera pokazuje nam jaka jest naprawdę, czyli idealnie okrągła.
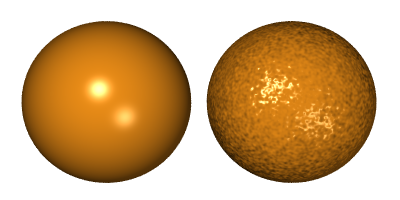
Źródło obrazka z wyrenderowanymi sferami oraz informacja o prawach autorskich: link.
Na poniższej ilustracji sytuacja (A) przedstawia płaską powierzchnię z wektorami normalnymi w różnych miejscach,
skoro powierzchnia jest płaska wszystkie te wektory mają ten sam kierunek. Sytuacja (B) przedstawia pofałdowaną powierzchnię.
Pofałdowanie powoduje, że wektory normalne mają różne kierunki. Sytuacja (C) przedstawia płaską powierzchnię,
w której prawdziwe wektory normalne zostały zastąpione wektorami z sytuacji (B), w efekcie czego obserwator ma wrażenie,
że widzi powierzchnię z sytuacji (B). Dlaczego tak się dzieje? Plastyczność powierzchni postrzegamy dzięki światłu,
które pada na powierzchnię, a następnie odbija się w kierunku naszych oczu.
Przy czym ilość odbitego światła silnie zależy od cosinusa kąta między wektorem normalnym a kierunkiem padania światła (nazwijmy go

Kodowanie i dekodowanie wektorów
Chcielibyśmy przechowywać w teksturze wektory,
którymi zastępowalibyśmy prawdziwe wektory normalne na teksturowanej powierzchni.
Wektory te możemy reprezentować jako trójki liczb rzeczywistych
Sposób dekodowania:
Poniżej fragmenty map wektorów normalnych użytych w programie dołączonym do artykułu. Dla tekstur zawierających wektory zakodowane w wyżej opisany sposób charakterystyczne są niebiesko-fioletowe barwy.



Podstawianie wektora normalnego
Wyobraźmy sobie punkt 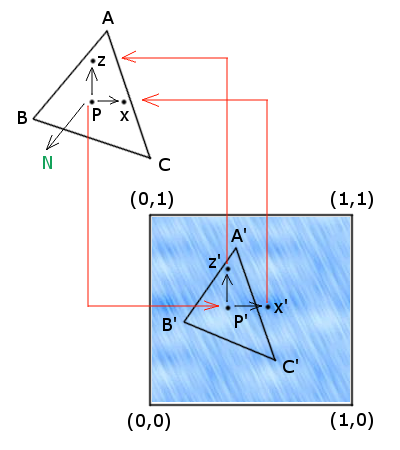 Mając punkt 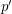 obliczamy punkty obliczamy punkty 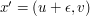 oraz oraz 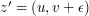 ,
gdzie ,
gdzie 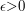 . Następnie obliczany współrzędne barycentryczne punktów . Następnie obliczany współrzędne barycentryczne punktów 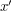 i i 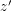 względem trójkąta względem trójkąta 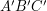 ,
wyznaczając przy ich pomocy punkty ,
wyznaczając przy ich pomocy punkty  i i  . Ostatecznie obliczamy wektory . Ostatecznie obliczamy wektory 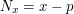 i i 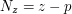 . .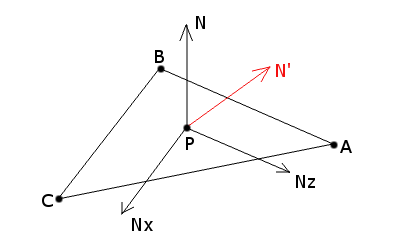 Niech ![$ v = \left[ \begin{array}{c} v_x \\ v_y \\ v_z \\ \end{array} \right] $](/files/tex/5a8029494803e68bf68e22f769e96c2bb2e04f80.png) będzie wektorem odkodowanym z tekstury.
Problem w tym, że jego współrzędne są w innym układzie współrzędnych niż punkt będzie wektorem odkodowanym z tekstury.
Problem w tym, że jego współrzędne są w innym układzie współrzędnych niż punkt  i wektor normalny i wektor normalny 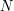 .
wektor .
wektor  można przedstawić jako kombinację liniową wektorów można przedstawić jako kombinację liniową wektorów
![$ E_x = \left[ \begin{array}{c} 1 \\ 0 \\ 0 \\ \end{array} \right] $](/files/tex/6dec53cd24587547cd8f0cd49b41a4c06b936b0a.png) , ,
![$ E_y = \left[ \begin{array}{c} 0 \\ 1 \\ 0 \\ \end{array} \right] $](/files/tex/e9a0516861f50eb26fa14bdafb8aa48cba39997f.png) , ,
![$ E_z = \left[ \begin{array}{c} 0 \\ 0 \\ 1 \\ \end{array} \right] $](/files/tex/0dec1c6cda9bbd0645d254190e445f903d495e50.png) ,
czyli ,
czyli 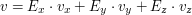 .
Wyobraźmy sobie, że obserwujemy świat z punktu .
Wyobraźmy sobie, że obserwujemy świat z punktu  ,
a nasze ciało ustawione jest tak, że wektor ,
a nasze ciało ustawione jest tak, że wektor 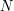 wskazuje nam kierunek w górę,
wektor wskazuje nam kierunek w górę,
wektor 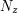 wskazuje nam kierunek na przód, a wektor wskazuje nam kierunek na przód, a wektor 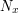 wskazuje nam kierunek w bok.
Możemy sobie wyobrazić, że punkt wskazuje nam kierunek w bok.
Możemy sobie wyobrazić, że punkt  jest teraz środkiem układu współrzędnych (punktem jest teraz środkiem układu współrzędnych (punktem 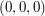 ),
a wektory ),
a wektory 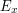 , , 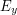 , , 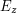 są wektorami bazowymi generującymi naszą przestrzeń, w takiej przestrzeni wyrażony jest nasz wektor są wektorami bazowymi generującymi naszą przestrzeń, w takiej przestrzeni wyrażony jest nasz wektor  .
Jeśli spojrzymy na całą sytuację z początku globalnego układu współrzędnych,
w którym umiejscowiony jest nasz trójkąt, punkt .
Jeśli spojrzymy na całą sytuację z początku globalnego układu współrzędnych,
w którym umiejscowiony jest nasz trójkąt, punkt  i wektor i wektor 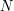 , to wektory , to wektory 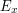 , , 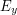 , , 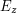 staną się wektorami kolejno staną się wektorami kolejno 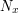 , , 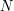 , , 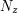 ,
zatem wektor ,
zatem wektor  w globalnym układzie współrzędnych (nazwijmy go w globalnym układzie współrzędnych (nazwijmy go 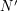 ) będzię kombinacją ) będzię kombinacją 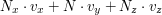 .
Teraz zamiast prawdziewgo wektora normalnego .
Teraz zamiast prawdziewgo wektora normalnego 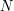 podczas obliczania oświetlenia używamy wektora podczas obliczania oświetlenia używamy wektora 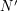 .
Podstawienia wektora dokonamy używając wywołania funkcji .
Podstawienia wektora dokonamy używając wywołania funkcji 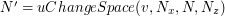 . .
Część I Część II Część III Część IV (2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 ),
który zależy od kierunku wektora normalnego oraz jego punktu zaczepienia.
Sytuacja (D) pokazuje, że jeśli pominiemy informację o zaczepieniu wektora normalnego umieszczając wektor normalny
z pofałdowanej powierzchni na płaskiej powierzchni,
to wbrew pozorom informacja o pofałdowaniu powierzchni będzie ciągle duża (ponieważ kąt
),
który zależy od kierunku wektora normalnego oraz jego punktu zaczepienia.
Sytuacja (D) pokazuje, że jeśli pominiemy informację o zaczepieniu wektora normalnego umieszczając wektor normalny
z pofałdowanej powierzchni na płaskiej powierzchni,
to wbrew pozorom informacja o pofałdowaniu powierzchni będzie ciągle duża (ponieważ kąt 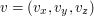 , gdzie
, gdzie ![$ v_x \in [-1, 1] $](/files/tex/05fc3e98661302a582f0b5d7b3c88f9f87aab0f9.png) ,
, ![$ v_y \in (0, 1] $](/files/tex/e675b3fd816c3e4bb4b870eb18a8a2fad9600620.png) ,
, ![$ v_z \in [-1, 1] $](/files/tex/28a54fea36bad319f1fb9c16dcd951836d37756d.png) (innymi słowy wektor
(innymi słowy wektor ![$ v \in [-1, 1] \times (0, 1] \times [-1, 1] $](/files/tex/69f18d353ebc14cde079c7699b789b3772b70087.png) ).
Pojedynczy tekstel
).
Pojedynczy tekstel  w teksturze reprezentowanej przez 24-bitową bitmapę ma postać
w teksturze reprezentowanej przez 24-bitową bitmapę ma postać  .
Widać tutaj wadę tego rozwiązania, wszystkich wektorów jest nieskończenie wiele,
natomiast przy użyciu 24-bitowej bitmapy jesteśmy w stanie zakodować skończenie wiele wektorów.
Jednak liczba wektorów jaką możemy zakodować wynosi
.
Widać tutaj wadę tego rozwiązania, wszystkich wektorów jest nieskończenie wiele,
natomiast przy użyciu 24-bitowej bitmapy jesteśmy w stanie zakodować skończenie wiele wektorów.
Jednak liczba wektorów jaką możemy zakodować wynosi 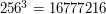 , co w praktyce jest zadowalające.
, co w praktyce jest zadowalające.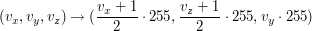
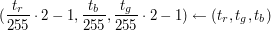
 na powierzchni trójkąta oraz wektor normalny
na powierzchni trójkąta oraz wektor normalny
 do tej powierzchni w punkcie
do tej powierzchni w punkcie 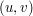 punktu
punktu 

