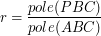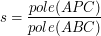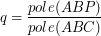Proces teksturowania
Zwykle mówi się o teksturowaniu obiektu lub nakładaniu tekstury na obiekt,
w rzeczywistości jednak obliczenia związane z teksturowaniem przypominają nakładanie obiektu na teksturę.
Punkt leżący na obiekcie mapujemy na układ współrzędnych tekstury (będzie to kwadrat ![$ [0,1]^2 $](/files/tex/70fc64cc7adba20f42360409e1448826d452b932.png) ).
).
Teksturowanie sfery
Reprezentacja sfery 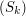 w kartezjańskim układzie współrzędnych:
w kartezjańskim układzie współrzędnych:
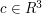 - środek sfery o współrzędnych
- środek sfery o współrzędnych 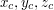
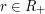 - promień sfery
- promień sfery
Reprezentacja sfery 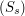 w sferycznym (biegunowym) układzie współrzędnych:
w sferycznym (biegunowym) układzie współrzędnych:
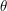 - kąt względem osi OX (tj. długość geograficzna)
- kąt względem osi OX (tj. długość geograficzna)
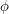 - kąt względem osi OY
(tj. szerokość geograficzna)
- kąt względem osi OY
(tj. szerokość geograficzna)
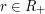 - promień sfery
- promień sfery
Więcej o współrzędnych sferycznych możesz przeczytać na wikipedii
Reprezentacje te są wzajemnie jednoznaczne.
Niech 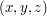 będzie punktem (w układzie kartezjańskim) na powierzchni sfery, a
będzie punktem (w układzie kartezjańskim) na powierzchni sfery, a 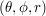 będą jego współrzędnymi biegunowymi.
Wtedy prawdziwa jest zależność:
będą jego współrzędnymi biegunowymi.
Wtedy prawdziwa jest zależność:
x = 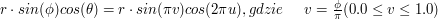
z = 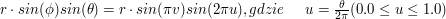
y = 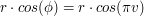
W ten sposób otrzymaliśmy mapowanie
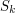
na
![$ [0, 1]^2 $](/files/tex/7a9f84f9de2770216ebaa0934142d559813716e8.png)
oraz mapowanie
![$ [0, 1]^2 $](/files/tex/7a9f84f9de2770216ebaa0934142d559813716e8.png)
na
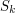
.
Mając współrzędne 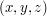 możemy wyznaczyć współrzędne
możemy wyznaczyć współrzędne 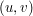 stosując powyższe wzory.
Musimy pamiętać, że aby użyć wzorów opisanych powyżej sefra musi mieć środek w początku układu współrzędnych.
Gwarantujemy to poprzez odjęcie środka sfery od punktu na sferze, dla którego obliczamy współrzędne w przestrzeni tekstury.
Dodatkowo trzeba uwzględnić w kodzie osobliwości we wzorach (miejsca, w których mogą wystąpić dzielenia przez 0
oraz miejsca, w których funkcja
stosując powyższe wzory.
Musimy pamiętać, że aby użyć wzorów opisanych powyżej sefra musi mieć środek w początku układu współrzędnych.
Gwarantujemy to poprzez odjęcie środka sfery od punktu na sferze, dla którego obliczamy współrzędne w przestrzeni tekstury.
Dodatkowo trzeba uwzględnić w kodzie osobliwości we wzorach (miejsca, w których mogą wystąpić dzielenia przez 0
oraz miejsca, w których funkcja 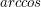 jest nieokreślona).
jest nieokreślona).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| // przekształcenie punktu z przestrzeni sfery na przestrzeń tekstury
inline vec2 mapSurfaceToTexture(sphere::i s, vec3::i p) {
vec3 lp = p - s.center;
float yDIVr = lp.y / s.radius;
float v =
( abs(yDIVr - 1.0f) < epsilon5 ) ? 0.0f : // v = 0 (górny biegun)
( abs(yDIVr + 1.0f) < epsilon5 ) ? 1.0f : // v = 1 (dolny biegun)
acos(yDIVr) / Pi; // bez osobliwości
float rMULsin = s.radius * sin(Pi*v);
float u = // 1,2 -> biegun // 3,4 -> |x/rMULsin|=1 -> acos nieokreślony
( abs(v) < epsilon5 ) ? 0.0f : // 1) (u,v) = (0.0, 0)
( abs(v - 1.0f) < epsilon5 ) ? 0.0f : // 2) (u,v) = (0.0, 1)
( abs(lp.x - rMULsin) < epsilon5 ) ? 0.0f : // 3) (u,v) = (0.0, v)
( abs(lp.x + rMULsin) < epsilon5 ) ? 0.5f : // 4) (u,v) = (0.5, v)
acos(lp.x / rMULsin) / PiMul2; // bez osobliwości
return vec2(u, v);
} |
Mając współrzędne 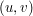 możemy również obliczyć współrzędne
możemy również obliczyć współrzędne 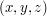 .
Musimy jedynie pamiętać, że po zastosowaniu wzorów do wyniku należy dodać środek sfery.
.
Musimy jedynie pamiętać, że po zastosowaniu wzorów do wyniku należy dodać środek sfery.
1
2
3
4
5
6
7
8
| // przekształcenie punktu z przestrzeni tekstury na przestrzeń sfery
inline vec3 mapTextureToSurface(sphere::i s, vec2::i p) {
return vec3(
s.center.x + s.radius * sin(Pi * p.v) * cos(PiMul2 * p.u),
s.center.y + s.radius * cos(Pi * p.v),
s.center.z + s.radius * sin(Pi * p.v) * sin(PiMul2 * p.u)
);
} |
Teksturowanie trójkąta
Trójkąt reprezentowany jest przez trójkę wierzchołków  ,
,  ,
, 
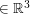 .
Dla wierzchołków tych musimy wyznaczyć punkty
.
Dla wierzchołków tych musimy wyznaczyć punkty 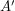 ,
, 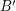 ,
, 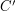
![$ \in [0,1]^2 $](/files/tex/63533133638eae3ae76036ef8a36182fa0786a56.png) ,
będące wierzchołkami naszego trójkąta w przestrzeni tekstury.
Dokonujemy tego zgodnie z naszymi upodobaniami co to tego gdzie powinien się znajdować nasz trójkąt w przestrzeni tekstury.
,
będące wierzchołkami naszego trójkąta w przestrzeni tekstury.
Dokonujemy tego zgodnie z naszymi upodobaniami co to tego gdzie powinien się znajdować nasz trójkąt w przestrzeni tekstury.
Następną rzeczą jaką potrzebujemy jest przepis na mapowanie dowolnego punktu trójkąta 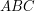 na odpowiadający mu punkt w trójkącie
na odpowiadający mu punkt w trójkącie 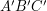 .
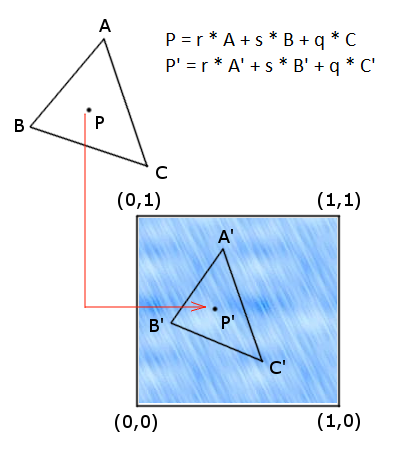
W tym celu wykorzystamy współrzędne barycentryczne. Niech
.
W tym celu wykorzystamy współrzędne barycentryczne. Niech 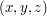 będą współrzędnymi kartezjańskimi punktu
będą współrzędnymi kartezjańskimi punktu  leżącego na trójkącie
leżącego na trójkącie 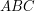 .
Obliczymy współrzędne
.
Obliczymy współrzędne 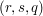 o właśności
o właśności 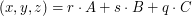 ,
, 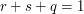 .
.
Używając współrzędnych barycentrycznych możemy w identyczny sposób przekształcać
współrzędne punktu na trójkącie pomiędzy przestrzenią trójwymiarową,
a przestrzenią tekstury. Wystarczy jedynie zastosować je do wierzchołków trójkąta
w odpowiedniej przestrzeni.
1
2
3
4
5
6
7
8
| // przekształcenie punktu z przestrzeni trójkąta na przestrzeń tekstury
inline vec2 mapSurfaceToTexture(triangle::i t, vec3::i p) {
float abc = area(t.v1 , t.v2 , t.v3);
float r = area( p , t.v2 , t.v3) / abc;
float s = area(t.v1 , p , t.v3) / abc;
float q = 1.0f - r - s;
return t.uv1*r + t.uv2*s + t.uv3*q;
} |
1
2
3
4
5
6
7
8
| // przekształcenie punktu z przestrzeni tekstury na przestrzeń trójkąta
inline vec3 mapTextureToSurface(triangle::i t, vec2::i p) {
float abc = area(t.uv1 , t.uv2 , t.uv3);
float r = area( p , t.uv2 , t.uv3) / abc;
float s = area(t.uv1 , p , t.uv3) / abc;
float q = 1.0f - r - s;
return t.v1*r + t.v2*s + t.v3*q;
} |
Poniżej pomocnicze w teksturowaniu funkcje obliczające pole trójkąta.
1
2
3
4
5
6
7
8
9
| // pole trójkąta rozpiętego w przestrzeni 3d na wierzchołkach v1, v2, v3
// implementacja wzoru Herona
inline float area(vec3::i v1, vec3::i v2, vec3::i v3) {
float a = length(v2 - v1);
float b = length(v3 - v1);
float c = length(v3 - v2);
float p = (a + b + c) / 2.0f;
return sqrt(p*(p-a)*(p-b)*(p-c));
} |
1
2
3
4
5
6
7
8
9
| // pole trójkąta rozpiętego w przestrzeni 2d na wierzchołkach v1, v2, v3
// implementacja wzoru Herona
inline float area(vec2::i v1, vec2::i v2, vec2::i v3) {
float a = length(v2 - v1);
float b = length(v3 - v1);
float c = length(v3 - v2);
float p = (a + b + c) / 2.0f;
return sqrt(p*(p-a)*(p-b)*(p-c));
} |




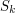 na
na ![$ [0, 1]^2 $](/files/tex/7a9f84f9de2770216ebaa0934142d559813716e8.png) oraz mapowanie
oraz mapowanie ![$ [0, 1]^2 $](/files/tex/7a9f84f9de2770216ebaa0934142d559813716e8.png) na
na 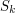 .
.



![$ [0,1]^2 $](/files/tex/70fc64cc7adba20f42360409e1448826d452b932.png) ).
).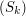 w kartezjańskim układzie współrzędnych:
w kartezjańskim układzie współrzędnych: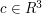 - środek sfery o współrzędnych
- środek sfery o współrzędnych 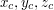
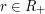 - promień sfery
- promień sfery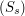 w sferycznym (biegunowym) układzie współrzędnych:
w sferycznym (biegunowym) układzie współrzędnych: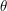 - kąt względem osi OX (tj. długość geograficzna)
- kąt względem osi OX (tj. długość geograficzna)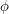 - kąt względem osi OY
(tj. szerokość geograficzna)
- kąt względem osi OY
(tj. szerokość geograficzna)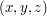 będzie punktem (w układzie kartezjańskim) na powierzchni sfery, a
będzie punktem (w układzie kartezjańskim) na powierzchni sfery, a 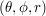 będą jego współrzędnymi biegunowymi.
Wtedy prawdziwa jest zależność:
będą jego współrzędnymi biegunowymi.
Wtedy prawdziwa jest zależność: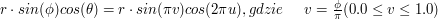
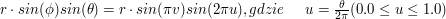
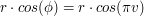
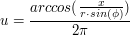
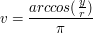
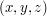 możemy wyznaczyć współrzędne
możemy wyznaczyć współrzędne 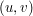 stosując powyższe wzory.
Musimy pamiętać, że aby użyć wzorów opisanych powyżej sefra musi mieć środek w początku układu współrzędnych.
Gwarantujemy to poprzez odjęcie środka sfery od punktu na sferze, dla którego obliczamy współrzędne w przestrzeni tekstury.
Dodatkowo trzeba uwzględnić w kodzie osobliwości we wzorach (miejsca, w których mogą wystąpić dzielenia przez 0
oraz miejsca, w których funkcja
stosując powyższe wzory.
Musimy pamiętać, że aby użyć wzorów opisanych powyżej sefra musi mieć środek w początku układu współrzędnych.
Gwarantujemy to poprzez odjęcie środka sfery od punktu na sferze, dla którego obliczamy współrzędne w przestrzeni tekstury.
Dodatkowo trzeba uwzględnić w kodzie osobliwości we wzorach (miejsca, w których mogą wystąpić dzielenia przez 0
oraz miejsca, w których funkcja 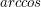 jest nieokreślona).
jest nieokreślona).
 ,
,  ,
, 
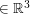 .
Dla wierzchołków tych musimy wyznaczyć punkty
.
Dla wierzchołków tych musimy wyznaczyć punkty 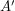 ,
, 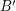 ,
, 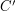
![$ \in [0,1]^2 $](/files/tex/63533133638eae3ae76036ef8a36182fa0786a56.png) ,
będące wierzchołkami naszego trójkąta w przestrzeni tekstury.
Dokonujemy tego zgodnie z naszymi upodobaniami co to tego gdzie powinien się znajdować nasz trójkąt w przestrzeni tekstury.
,
będące wierzchołkami naszego trójkąta w przestrzeni tekstury.
Dokonujemy tego zgodnie z naszymi upodobaniami co to tego gdzie powinien się znajdować nasz trójkąt w przestrzeni tekstury.
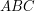 na odpowiadający mu punkt w trójkącie
na odpowiadający mu punkt w trójkącie 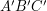 .
W tym celu wykorzystamy współrzędne barycentryczne. Niech
.
W tym celu wykorzystamy współrzędne barycentryczne. Niech  leżącego na trójkącie
leżącego na trójkącie 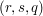 o właśności
o właśności 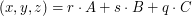 ,
, 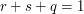 .
.