Zabawa z drzewami
15.12.2009 - Łukasz Zatorski
 „Głupiec i mędrzec nie widzą tego samego drzewa.” - mawiał William Blake. Drzewa dostarczają życiodajnego tlenu, w słoneczny dzień służą cieniem, a ich abstrakcyjne odpowiedniki są nieodzownym elementem arsenału dobrego programisty. Tylko, no właśnie, o czym dokładnie mowa i jak się do tego zabrać? W poszukiwaniu kilku klasycznych problemów informatycznych dotyczących drzew zapraszam do... Puszczy Amazońskiej. W końcu, jeśli nie w lesie szukać drzew, to gdzie? Nasza odpowiedź nie będzie jednak tak oczywista, jakby się wydawało. Skupimy się na sercu każdej tropikalnej puszczy – rzece. W nieprzebytych i niezbadanych lasach, często jest ona jedyną znaną drogą i szybkim źródłem transportu między położonymi przy niej siedzibami plemion. Jeśli weźmiemy pod uwagę fragment jej dorzecza, w którym dopływy nie tworzą cyklu, a leżące nad nią wioski uznamy za wierzchołki grafu, spełnimy wszystkie konieczne wymagania by powstałą przez nas strukturę nazwać drzewem.
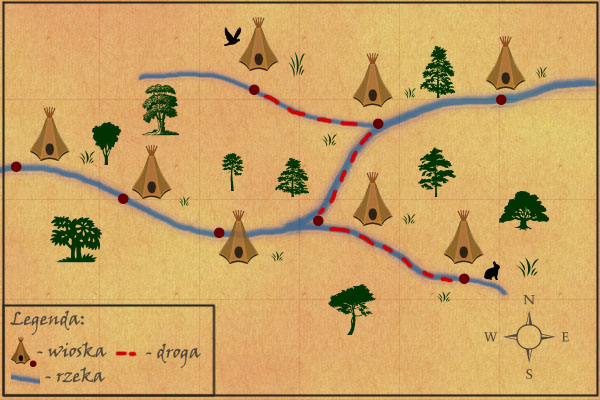
Między każdymi dwoma wierzchołkami wiedzie dokładnie jedna droga. Gdzie tkwi problem:Rozważmy lekarza działającego w ramach misji WHO1. Postanawia on założyć szpital w jednej z wiosek, do którego w razie pilnego przypadku (czyli takiego z którym nie potrafią sobie poradzić plemienni znachorzy) przybywałyby rzeką osoby potrzebujące z innych plemion. Załóżmy na razie, że wioski położone są od siebie w równych odległościach (w celu uniknięcia wojen terytorialnych, sprawiedliwie podzielono wybrzeża). Oczywistym jest, że wybór miejsca na szpital nie powinien być przypadkowy – w kwestii ratowania ludzkiego życia, czas ma ogromne znaczenie. Interesuje nas więc, by odległość szpitala do najdalszej wioski, była możliwie najmniejsza.
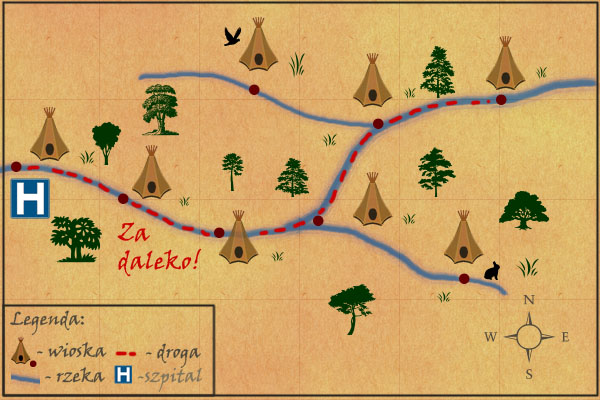
Ta wioska nie nadaje się na szpital! Stojące przed nami zadanie jest popularnym w algorytmice problemem optymalizacyjnym. W tym przypadku za kryterium wyboru uznajemy najgorszą możliwą sytuację, tzn. konieczność udzielenia pomocy osobie z najdalej położonej wioski. Kryterium to będziemy dla ułatwienia nazywać „postawą lekarza”.
Czy potrafisz znaleźć wierzchołek centralny drzewa po lewej?
Skoro intuicyjna metoda poszukiwania rozwiązania nie sprawdza się w przypadku większych drzew, spróbujmy zapisać ją pod postacią jakiegoś algorytmu. Z pewnością pierwsze co zrobiłeś, to wykluczyłeś wszystkie liście.
Obserwacja:
Spróbujmy zatem dalej postępować drogą eliminacji. Mając dane drzewo T1, odetnijmy wszystkie liście naraz i zobaczmy co się stało:
Żaden z liści nie mógł być wierzchołkiem centralnym, zatem zgodnie z naszą obserwacją nadal znajduje się on nowo powstałym drzewie T2. Co więcej:
Oznacza to, że poprzez usunięcie liści, wartość najdłuższej ścieżki od każdego wierzchołka zmniejszyła się dokładnie o jeden. Skoro wszystkim zabraliśmy tyle samo, w takim razie wierzchołek centralny drzewa T1 i T2 „nie zmienił swojego miejsca” - to nadal ten sam wierzchołek! Nie pozostaje nic innego, jak powtórzyć rekurencyjnie nasz algorytm. Z radością bierzemy więc do ręki nożyczki i ponownie tniemy, i tniemy, i tniemy, i... chwila, chwila, nie rozpędzajmy się!
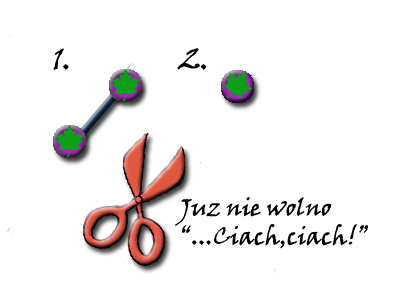
No właśnie, każda przyjemność kiedyś się kończy. W momencie kiedy drzewo Tn składa się z samych liści, dokonanie cięcia nie jest już możliwe, lub spowoduje, że pozbędziemy się wszystkich wierzchołków. Rysunek obok przedstawia dwie możliwe sytuacje końcowe. Oczywiście otrzymany wynik to wierzchołki centralne – dowiedliśmy tym samym, że czasem drzewo może posiadać dwa (ale zawsze sąsiadujące ze sobą).
Załóżmy że posiadamy już listę wierzchołków naszego drzewa. Jak zaimplementować taki algorytm?
Dla chętnych:
Dla każdej krawędzi i każdego wierzchołka w naszym algorytmie wykonujemy stałą liczbę operacji, zatem jego złożoność jest liniowa względem wielkości danych (mówimy też, że należy do klasy
(11 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



 Wierzchołek
którego szukamy to intuicyjnie ten „najbliżej środka” -
nazywany również wierzchołkiem centralnym drzewa. Myślę że
błyskawicznie udało Ci się go odnaleźć na mapie wiosek z naszego
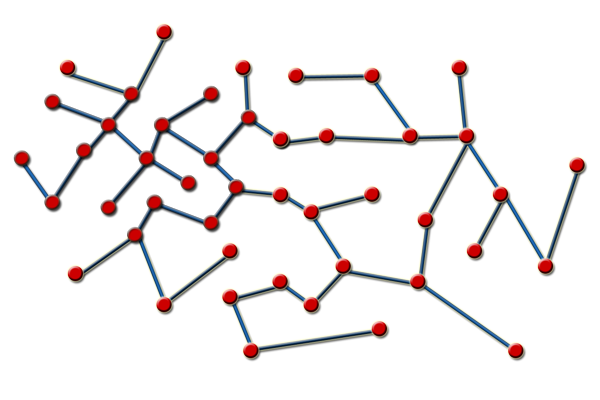
przykładu. Jednak w sytuacji, kiedy trzeba zmierzyć się z dużo
większymi danymi, odpowiedź nie jest już taka oczywista.
Wierzchołek
którego szukamy to intuicyjnie ten „najbliżej środka” -
nazywany również wierzchołkiem centralnym drzewa. Myślę że
błyskawicznie udało Ci się go odnaleźć na mapie wiosek z naszego
przykładu. Jednak w sytuacji, kiedy trzeba zmierzyć się z dużo
większymi danymi, odpowiedź nie jest już taka oczywista.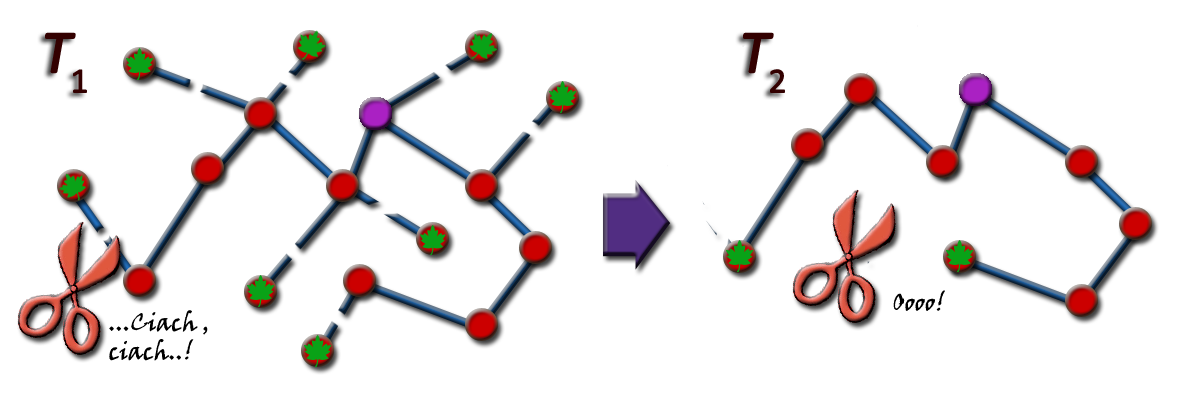
 możemy wyznaczyć jego stopień (przyjmijmy
oznaczenie
możemy wyznaczyć jego stopień (przyjmijmy
oznaczenie ![$ DEG[v] $](/files/tex/71083dd7f584ec41965cbc7fdd76ce5edb9f4aec.png) ).
).
![$ DEG[v]=1 $](/files/tex/2be66d0647d11d396b00826c7872fa968cf74b3d.png) ) umieszczamy we wspólnej kolejce
) umieszczamy we wspólnej kolejce 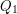 – aktualną porcję liści do usunięcia.
– aktualną porcję liści do usunięcia.
 )
)
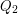 (oznacza to, że jest liściem do usunięcia w ,,następnej rundzie")
(oznacza to, że jest liściem do usunięcia w ,,następnej rundzie")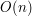 ).
).

