Zabawa z drzewami
15.12.2009 - Łukasz Zatorski
 Im dalej w las, tym więcej drzew:Wierzchołek centralny nie jest niestety uniwersalną odpowiedzią na wszystkie pytania optymalizacyjne. Rozwiązania zależą od podjętego przez nas kryterium. Przykładowo - wysyłanie codziennie dzieci do szkoły nie bardzo podobałoby się wodzom – wyraźnie destabilizuje to życie plemienne. Dlatego nauczyciele UNESCO korzystając z motorówek, każdego dnia odwiedzają którąś z wiosek i na noc wracają do bazy. Czas dojazdu nie jest aż tak istotny – w przypadku zaplanowanych wizyt nie trudno wyruszyć odpowiednio wcześniej. Większy problem stanowi natomiast zużycie paliwa – nauczyciele gotowi są przenieść swoją siedzibę w lepiej usytuowane miejsce, a za zaoszczędzone w ten sposób pieniądze woleliby kupić podręczniki i materiały do nauki. Zauważmy, że nauczycieli interesuje możliwie najniższe średnie zużycie paliwa na jedną podróż. Postawa ta oznacza w szczególności, że myślą bardziej globalnie i są czasem gotowi na daleką i kosztowną wyprawę, jeśli średni przypadek dzięki temu będzie mniejszy.
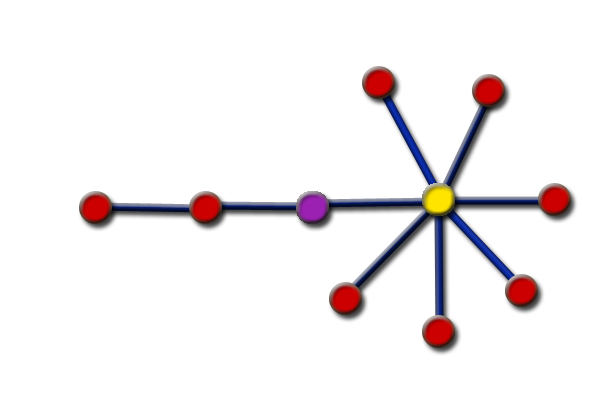
Drzewo po prawej przedstawia możliwość istnienia różnicy między postawą lekarza (preferowany wierzchołek - fioletowy), a postawą nauczyciela (preferowany wierzchołek - żółty).
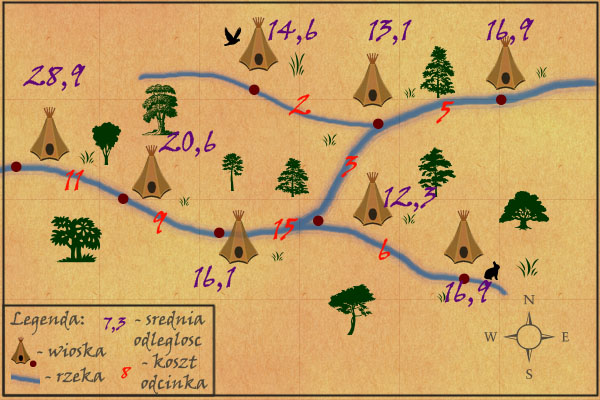
Na dodatek, zużycie paliwa nie musi być na każdym odcinku koniecznie takie samo – zależy ono min. od siły prądu na danym fragmencie rzeki, czy głębokości koryta – uzupełniamy zatem nasz graf o wagi na jego krawędziach, a za odległość między dwoma wioskami uznajemy sumę krawędzi na łączącej je ścieżce. Metoda z obcinaniem liści nie bierze pod uwagę krawędzi, dlatego potrzebujemy świeżego podejścia.
Mapa z wioskami i wskaźnikami zużycia paliwa na trasie. Jak zatem wyznaczyć dla danego wierzchołka Obserwacja:
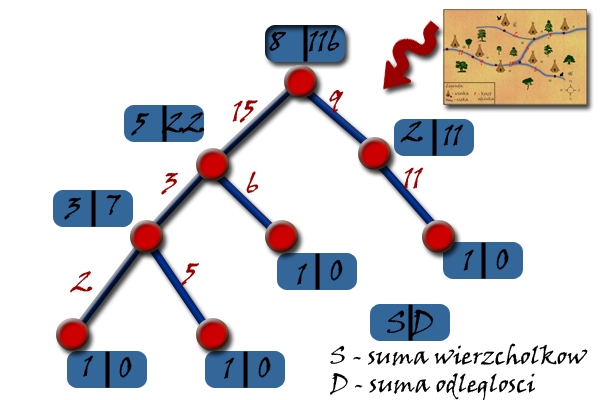
Dla danego drzewa, ilość wierzchołków nie zmienia się w trakcie wykonywanego algorytmu, dlategonasze kryterium możemy utożsamiać z najmniejszą sumą odległości do pozostałych wierzchołków. Zauważmy, że sumując po kolei odległości do wszystkich wierzchołków, każdą krawędź liczymy wielokrotnie. Częstość użycia krawędzi zależy od ilości wierzchołków w poddrzewie, do którego ona prowadzi. Na rysunku obok krawędź między wierzchołkami 3 i 5 liczymy trzykrotnie - jako fragment drogi do wierzchołków 1,2,3. Ukorzenione drzewo ma w naturalny sposób zdefiniowaną strukturę rekurencyjną. Niezależnie od użytej metody przeszukiwania (BFS, DFS), możliwe jest korzystanie z zależności między rodzicem a synem. Niech
Konstruujemy zależność rekurencyjną: 1. Dla
liści drzewa: 2. Dla wierzchołka wewnętrznego:
(każda droga jest
dotychczasową drogą do Jeśli
zastosujemy tę zależność przy algorytmie przeszukiwania DFS dla każdego z wierzchołków z osobna, otrzymamy
złożoność rzędu:
Załóżmy
zatem, że policzyliśmy wielkość
Widzimy że część dróg ulega wydłużeniu, a część skróceniu. Do
Teraz możemy powtórzyć naszą operację dla synów wierzchołka
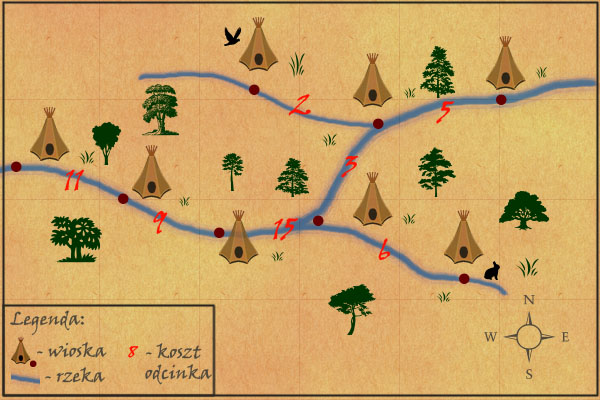
Mapa z zaznaczonymi średnimi odległościami dla każdej z wiosek. Jeśli dotrwałeś do tego miejsca, drogi czytelniku – gratuluję! Wiesz już zatem jak znaleźć punkty szczególne i poznałeś tym samym podstawowe rodzaje sposobów i podejść do problemów informatycznych związanych z drzewami. Gorąco zachęcam do odprężającego spaceru w parku w ramach odpoczynku od komputera, a następnie proponuję zmierzyć się z zadaniami umieszczonymi na portalu :)
1 - Więcej o światowej organizacji zdrowia i jej misjach możesz przeczytać na http://www.who.int/. (11 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 jego średnią odległość do pozostałych?
jego średnią odległość do pozostałych?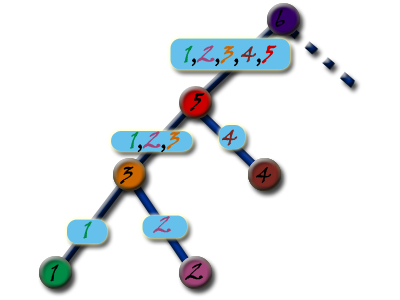
![$ D[v] $](/files/tex/b3426e1d490d4f59bf10faee6172d5c411322f95.png) oznacza sumę odległości do korzenia w poddrzewie
wyznaczonym przez wierzchołek
oznacza sumę odległości do korzenia w poddrzewie
wyznaczonym przez wierzchołek ![$ S[v] $](/files/tex/6064f5cfe14609b6ceb2b6027de8a93ac66138bd.png) – ilość wierzchołków
w tym poddrzewie,
– ilość wierzchołków
w tym poddrzewie, 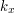 - wagę krawędzi do wierzchołka
- wagę krawędzi do wierzchołka  .
.![$ D[v]:=0, S[v]:=1 $](/files/tex/fd6144b530c3752e899980cc121a139e6933fb9a.png)
![$ S[v]:= 1+ \sum_{x \in child(v)} S[x] $](/files/tex/2cda42c36989bb5b29804308da581618dbad436a.png)
![$ D[v] =\sum_{x \in child(v)} (S[x] * k_x + D[x]) $](/files/tex/3b6bea9e2e535ac5b4d7f28f9de5e92e15c6378c.png)
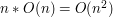 . Wielkość ta nas nie
zadowala – możemy odnieść wrażenie, że nie wykorzystujemy w
pełni wszystkich posiadanych informacji – w końcu rozwiązania
dla wierzchołków które znajdują się blisko, intuicyjnie powinny
być zbliżone. Dlatego po obliczeniu rozwiązania dla jednego
wierzchołka, spróbujmy ponownie wykorzystać zależność
rekurencyjną, ale teraz w odwrotnym kierunku – tzn. „jaki
ojciec, taki syn”.
. Wielkość ta nas nie
zadowala – możemy odnieść wrażenie, że nie wykorzystujemy w
pełni wszystkich posiadanych informacji – w końcu rozwiązania
dla wierzchołków które znajdują się blisko, intuicyjnie powinny
być zbliżone. Dlatego po obliczeniu rozwiązania dla jednego
wierzchołka, spróbujmy ponownie wykorzystać zależność
rekurencyjną, ale teraz w odwrotnym kierunku – tzn. „jaki
ojciec, taki syn”.![$ S[] $](/files/tex/264160107b15b42c3a683e1b2ecb386ec195e03c.png) . Co stanie się teraz,
kiedy przeniesiemy bazę nauczycieli do jego syna
. Co stanie się teraz,
kiedy przeniesiemy bazę nauczycieli do jego syna 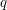 ?
?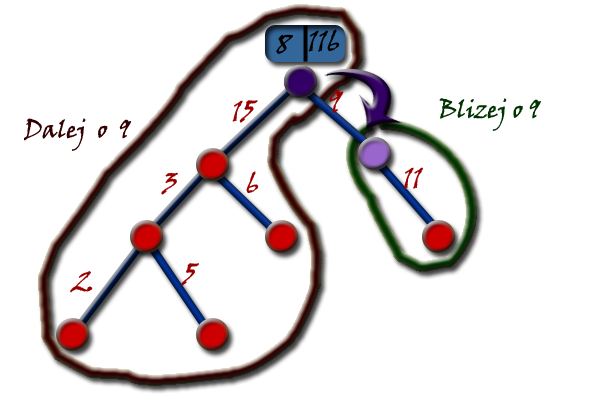
![$ S[q] $](/files/tex/9b4273307472edd293ecf8fc68ef39e86704d109.png) wierzchołków mamy bliżej o wartość
wierzchołków mamy bliżej o wartość 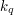 , natomiast odległość
do pozostałych
, natomiast odległość
do pozostałych ![$ N – S[q] $](/files/tex/278e57c9ea77a9407cddc2eae4e3b9f630c293c5.png) wierzchołków zwiększyła się o tę wartość. Tym samym możemy wyznaczyć:
wierzchołków zwiększyła się o tę wartość. Tym samym możemy wyznaczyć:![$ D[q]=D[v]+k_q*(N–S[q])–k_q*S[q] $](/files/tex/df13f4b9806c36d04b8f3595578bf74e77e70470.png)
![$ =D[v]+k_q*(N–2*S[q]) $](/files/tex/62233c5c6f15297dda8dc96f306e026db9506f0a.png)
![$ D[] $](/files/tex/688469094bbf9f1dbf156e0fd2b85502084347d3.png) jest oczywiście najlepszym miejscem na założenie bazy dla
nauczycieli.
jest oczywiście najlepszym miejscem na założenie bazy dla
nauczycieli.