Zabawa z drzewami
15.12.2009 - Łukasz Zatorski
 ŚrednicaLimit czasowy: 12s; Limit pamieciowy: 64MB;
Średnicą drzewa nazywamy odległość między dwoma najdalszymi wierzchołkami. Dla zadanego drzewa, znajdź liczbę krawędzi na ścieżce łączącej takie dwa wierzchołki. Wejście:
W pierwszej linii wejścia znajduje się liczba całkowita Wyjście: Jedna liczba całkowita - ilość krawędzi na najdłuższej ścieżce w drzewie. Przykład: Wejście: 9 5
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
JaskiniaLimit czasowy: 13s; Limit pamięciowy: 32MB;
Jaskinia jest siecią wydrążonych w skale komór i łączących ich korytarzy. Oczywiście, nie każda jaskinia jest wystarczająco mokra i brudna by nadawać się na siedzibę trolli. Te paskudne stworzenia nie słyną również z wysokiej inteligencji, i potrafią zgubić się w ciemnościach i chodzić w kółko tygodniami. Koniecznym jest zatem, by między każdymi dwoma komorami dało się dojść dokładnie na jeden sposób. Pewna rodzina trolli wybrała już sobie jaskinię spełniającą te kryteria, jednak nie wiedzą, czy będzie ona wystarczająco komfortowa, by ich pomieścić. Trolle darzą niechęcią nawet swoich braci i siostry - by znieść swoje wzajemne towarzystwo, wytyczają łańcuch komór i korytarzy, nazywany "Głównym holem", a każdy łączący się z nim fragment jaskini, zwany "siedliskiem" w miarę możliwości przydziela się tylko jednemu trollowi. Rodzina trolli chciałaby wiedzieć, jaką maksymalną liczbę siedlisk można w ten sposób uzyskać - niestety samo liczenie do trzech powoduje już u nich zawroty głowy. Dlatego postanowiły one rozwiązać to zadanie algorytmem typu Brute Force - zagroziły, że jeżeli zaraz im nie pomożesz, to wezmą swoje maczugi i zrobią... no właśnie, nie masz najmniejszego zamiaru dowiadywać się co Ci zrobią. Wejście:
W pierwszej linii wejścia znajduje się liczba całkowita Wyjście: Jedna liczba całkowita - maksymalna liczba siedlisk jaką da się wytyczyć metodą stosowaną przez trolle. Uwaga: Główny hol musi zaczynać się i kończyć w jakiejś komorze, w szczególności może się składać wyłącznie z jednej komory. Przykład: Wejście: 10 Wyjście: 6
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. (11 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com



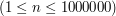 . W kolejnych
. W kolejnych 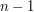 liniach znajdują się pary liczb całkowitych
liniach znajdują się pary liczb całkowitych 

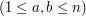 , oznaczających, że wierzchołek o numerze
, oznaczających, że wierzchołek o numerze 

