Query on a tree III
19.02.2010 - Wiktor Janas
    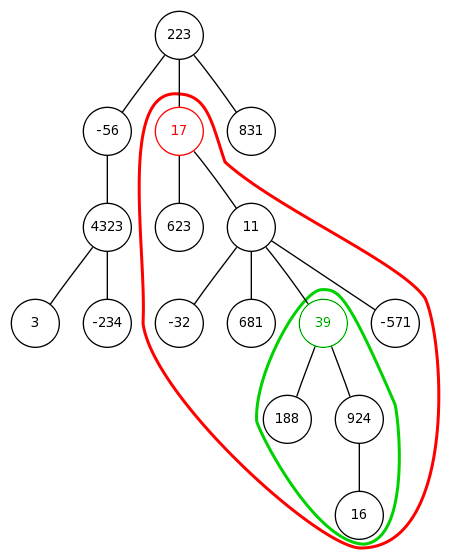 Dane jest ukorzenione drzewo z etykietowanymi wierzchołkami. Należy odpowiadać na zapytania "który wierzchołek z poddrzewa wierzchołka v ma k-tą największą etykietę". Ilość wierzchołków n ≤ 100.000, ilość zapytań q ≤ 10.000. Etykiety są dowolnie duże oraz parami różne. Przykładowe drzewo oraz dwa zapytania na nim przedstawia rysunek obok (liczby w wierzchołkach są etykietami, nie numerami wierzchołków). W poddrzewie "czerwonym" ósmą największą etykietą jest 623, natomiast w poddrzewie "zielonym" drugą największą etykietą jest 39. Najprostszym rozwiązaniem byłoby oczywiście dla każdego zapytania posortować zbiór wierzchołków odpowiedniego poddrzewa i wybrać z niego k-ty element. Niestety pesymistycznie algorytm taki działałby w czasie O(q n log n), czyli wykonywał ponad miliard operacji. Zdecydowanie zbyt długo. Dane jest ukorzenione drzewo z etykietowanymi wierzchołkami. Należy odpowiadać na zapytania "który wierzchołek z poddrzewa wierzchołka v ma k-tą największą etykietę". Ilość wierzchołków n ≤ 100.000, ilość zapytań q ≤ 10.000. Etykiety są dowolnie duże oraz parami różne. Przykładowe drzewo oraz dwa zapytania na nim przedstawia rysunek obok (liczby w wierzchołkach są etykietami, nie numerami wierzchołków). W poddrzewie "czerwonym" ósmą największą etykietą jest 623, natomiast w poddrzewie "zielonym" drugą największą etykietą jest 39. Najprostszym rozwiązaniem byłoby oczywiście dla każdego zapytania posortować zbiór wierzchołków odpowiedniego poddrzewa i wybrać z niego k-ty element. Niestety pesymistycznie algorytm taki działałby w czasie O(q n log n), czyli wykonywał ponad miliard operacji. Zdecydowanie zbyt długo.
Załóżmy na chwilę, że jeżeli musimy odpowiedzieć na zapytanie dla wierzchołka q1, to na ścieżce z q1 do korzenia drzewa nie ma już żadnych zapytań. W takim wypadku powyższy algorytm nigdy nie przetworzy jednego wierzchołka dwa razy (ponieważ ten sam wierzchołek nigdy nie występuje w poddrzewach dwóch różnych zapytań). Zatem ilość wykonywanych operacji to tylko O(n log n)! Jasno widać zatem słabość naszego rozwiązania – jeżeli odpowiedzieliśmy na zapytanie w wierzchołku v oraz istnieje zapytanie o poddrzewo wierzchołka u, który leży gdzieś na ścieżce z v do korzenia, to odpowiadając na zapytanie w u wierzchołki z poddrzewa v przetworzymy ponownie. 
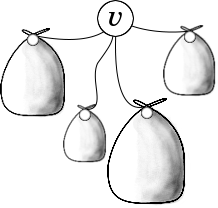
Potrzebna byłaby struktura danych przechowująca zbiór elementów, umożliwiająca wybieranie k-tego z nich oraz dodawanie nowych. Używając jej moglibyśmy odpowiadać na zapytania w kolejności ich występowania w drzewie. Odpowiadając na zapytanie w wierzchołku v zaczęlibyśmy od przetworzenia wszystkich poddrzew v (rysunek po lewej). Otrzymane w ten sposób zbiory elementów w poddrzewach połączylibyśmy w nowy zbiór i dodali przetwarzany wierzchołek v (rysunek po prawej). W ten sposób powstałby zbiór wszystkich wierzchołków poddrzewa v, z którego dałoby się szybko wyciągnąć k-ty element. Zadowalająca nas struktura danych to na przykład drzewa czerwono-czarne. Oczywiście ich najsilniejszym atutem jest to, że nie trzeba ich implementować – gotową (i działającą!) implementacją jest bowiem struktura set<> z biblioteki STL. Żeby jednak nie było zbyt pięknie trzeba dodać, że owa implementacja nie umożliwia szybkiego wybierania k-tego elementu (chociaż jest to możliwe z wykorzystaniem drzew czerwono-czarnych). Można pokusić się o zaimplementowanie drzew AVL – jest to prostsza struktura danych o podobnych możliwościach. Okazuje się jednak, że do naszych celów wystarczające będą zwykłe drzewa licznikowe. 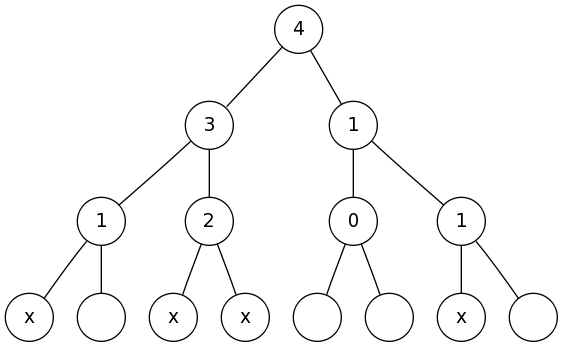
Drzewo licznikowe to zrównoważone drzewo binarne. W jego liściach pamiętamy elementy, które mogą znaleźć się w przechowywanym zbiorze (to znaczy nie tylko te, które już dodaliśmy – musimy zrobić miejsce dla wszystkich elementów, które kiedykolwiek zechcemy dodać), w kolejności posortowanej (to znaczy najmniejszy element będzie w pierwszym liściu, a największy w ostatnim). W pozostałych wierzchołkach pamiętamy, ile elementów jest w ich poddrzewach. Dodawanie elementu jest proste: mamy już zarezerwowane miejsce na element, zatem wystarczy oznaczyć je jako "zajęte" oraz przejść ścieżką do korzenia zwiększając liczniki w każdym wierzchołku. Jeżeli drzewo może pamiętać n elementów, operacja ta potrwa O(log n), ponieważ tyle właśnie pięter drzewa dzieli liście od korzenia. Wyszukiwanie k-tego element również jest proste. Rozpoczynamy z korzenia i spoglądamy na lewego i prawego syna. Każdy z nich pamięta, ile elementów jest w jego poddrzewie (niech będą to odpowiednio a oraz b). Co więcej, wszystkie elementy z poddrzewa lewego syna są mniejsze od elementów z poddrzewa prawego syna. Zatem jeżeli zachodzi k < a, to szukany element z pewnością znajduje się w poddrzewie lewego syna. W przeciwnym wypadku poszukujemy (k-a)-tego elementu w poddrzewie prawego syna. W powyższych rachunkach wygodnie jest, aby k=0 oznaczało najmniejszy element oraz aby drzewo było pełne, tzn. ilość jego liści była potęgą dwójki. Jak widać wykonujemy tylko jedną operację na każdy poziom drzewa, zatem wyszukiwanie k-tego elementu również trwa O(log n). Uzbrojeni w tak wspaniałe narzędzia powróćmy do zadania. Jakie elementy chcielibyśmy pamiętać w drzewie licznikowym? Prawdopodobnie pary (etykieta,wierzchołek). Ponieważ porównujemy takie pary tylko po etykietach, wystarczy zarezerwować w drzewie jednego liścia dla każdej możliwej etykiety. Aby nie było zbyt wspaniale przypominamy, że mogą one być dowolnie duże (no dobrze, powiedzmy że z zakresu -1.000.000.000 do +1.000.000.000). Czy to przekreśla nasze rozwiązanie? Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
|
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




