Query on a tree III
19.02.2010 - Wiktor Janas
    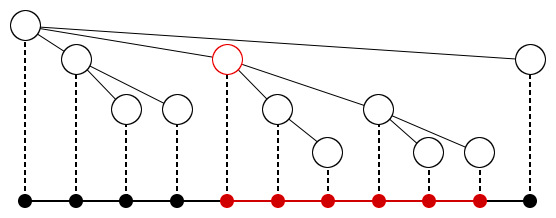
Jedną ze znanych operacji, jakie można wykonać na drzewie, jest przekształcenie go do odcinka, to znaczy wypisanie wszystkich wierzchołków w porządku pre-order lub post-order. Jeżeli potraktowalibyśmy nasze drzewo w ten sposób, problem znalezienia k-tego elementu w poddrzewie v sprowadza się do problemu znalezienia k-tego elementu na pewnym pod-odcinku (ponieważ każde poddrzewo w porządku pre-order jest spójnym odcinkiem). Zamienienie drzewa na odcinek oraz wyznaczenie zakresów pod-odcinków (tzn. gdzie zaczyna się, a gdzie kończy zapis każdego poddrzewa) jest proste. Gdybyśmy mieli odpowiadać na wiele zapytań postaci "znajdź k-ty elementy na odcinku", moglibyśmy użyć opisanego wcześniej drzewa licznikowego. Musimy jednak udoskonalić to rozwiązanie, aby móc również znajdować k-ty element na pod-odcinkach. W tym celu w korzeniu naszego drzewa zapamiętamy numery wszystkich elementów z odcinka (dokładnie w takiej kolejności, w jakiej występują na odcinku – czyli po prostu 0,1,2,...,n-1). Następnie w lewym synu zapamiętamy numery elementów mniejszych od mediany, a w prawym większych od mediany (wciąż w takiej kolejności, jak na odcinku). Dzięki temu lewy i prawy syn będą zawierali po połowie elementów ojca oraz wszystkie elementy z lewego syna będą mniejsze od elementów z prawego – podobnie jak w drzewie licznikowym. Oczywiście będziemy dzielić w ten sposób rekurencyjnie, aż dojdziemy do zbiorów jednoelementowych. Zauważmy, że każdy element będzie pamiętany tylko w log n "kubełkach", zatem rozmiar całego drzewa będzie O(n log n). Podzielnie jednego kubełka na dwa wymaga O(n) operacji, ponieważ medianę potrafimy znaleźć w czasie liniowym, dalej zaś wystarczy przejrzeć wszystkie elementy z kubełka i dodać je do lewego lub prawego, w zależności od tego czy są mniejsze czy większe od znalezionej mediany (ważne jest, aby w kubełkach zachować kolejność taką, jak na odcinku). Zatem zbudowanie całego drzewa będzie wymagało czasu proporcjonalnego do jego rozmiaru, czyli również O(n log n). 
Konstrukcję struktury dla przykładowego odcinka przedstawia rysunek powyżej. W pierwszym kubełku zapamiętujemy indeksy wszystkich elementów odcinka. Medianą wartości na odcinku jest 2 (zaznaczona na czerwono), zatem w lewym kubełku znajdą się indeksy elementów mniejszych od 2, w prawym zaś pozostałe. Gruba linia podziału oznacza, że dokonujemy podziału kubełka, cienka że dokonaliśmy podziału wcześniej. Zauważ, że indeksy w jednoelementowych kubełkach na samym dole odpowiadają posortowanemu ciągowi wyjściowemu. Jak przy użyciu takiej struktury znaleźć k-ty element na pod-odcinku? W korzeniu pamiętamy wprawdzie cały odcinek, ale używając wyszukiwania binarnego możemy prosto znaleźć przedział, który zawiera tylko elementy z interesującego nas pod-odcinka (ponieważ pamiętamy numery elementów, a nie ich wartości). Gdybyśmy zatem w myślach znaleźli takie przedziały w każdym kubełku i zapomnieli o tym, że są tam również inne elementy, nasza struktura okazałaby się drzewem licznikowym dla pod-odcinka. W takim zaś znaleźć k-ty element już potrafimy. Na rysunku powyżej kolorem niebieskim zaznaczono we wszystkich kubełkach przedziały, które odpowiadają przykładowemu pod-odcinkowi. Koszt pojedynczego wyszukiwania to O(log n log n) ponieważ postępujemy tak samo jak dla drzewa licznikowego z tym, że w każdym kroku musimy wykonać dwa wyszukiwania binarne, aby zawęzić kubełek do interesującego nas przedziału. Pozostaje kwestia znalezienia mediany (czyli k-tego elementu dla k=s/2, gdzie s jest rozmiarem kubełka) w kubełku. Tym razem nie potrzebujemy żadnej struktury danych, ponieważ jest to tylko jedno zapytanie. Działającym liniowo algorytmem wyszukiwania mediany jest algorytm magicznych piątek. Nam wystarczy jego uboższy kuzyn, algorytm Horae’a (którego oczekiwany czas działania jest liniowy, ale pesymistyczny – kwadratowy). Algorytm ten jest bardzo podobny do algorytmu quicksort (również odkrytego przez Hoare’a). Szukamy k-tego elementu w s-elementowym kubełku. Wybieramy losowo element z kubełka, a następnie przesuwamy wszystkie elementy mniejsze na lewo od niego, a większe na prawo (jest to znana z quicksorta operacja partition). Jeżeli wybrany element wypadł na pozycji a, która jest większa od k, to rekurencyjnie szukamy k-tego elementu wśród pierwszych a elementów, w przeciwnym razie szukamy (k-a)-tego elementu wśród ostatnich s-a elementów. Każdy przebieg algorytmu kosztuje nas liniowo od rozmiaru kubełka, jednak oczekujemy, że rozmiary przeszukiwanego obszaru będą malały o połowę przy każdej iteracji. Dlatego średni czas działania algorytmu jest liniowy. Biblioteka STL zawiera implementacje algorytmu Hoare’a pod nazwą nth_element. Okazuje się, że krok wyszukiwania mediany można wyeliminować. Przypuśćmy, że niezależnie od kubełków dysponujemy również ciągiem indeksów w koleności rosnących wartości (na przykładzie z rysunku byłby to ciąg 0,3,1,5,6,9,4,2,8,7). Mając tę informację znalezienie mediany jest trywialne - indeks mediany będzie bowiem znajdował się na środku owego ciągu. Możemy zatem podobnie jak wcześniej obliczyć zawartość lewego i prawego kubełka na pierwszym poziomie. Zauważmy teraz, że liczby, które trafia do lewego kubełka w ciągu posortowanym będą znajdowały się w pierwszej połowie, natomiast liczby z prawego kubełka - w drugiej połowie. Zatem indeksy znajdujące się w jednym kubełku zawsze tworzą spójny fragment w ciągu posortowanych indeksów. Co więcej, określenie tego fragmentu jest proste - zatem potrafimy znajdować medianę do podziału kubełka w czasie stałym! Ostatnim usprawnieniem opisywanego algorytmu będzie pozbycie się wyszukiwania binarnego z procedury odpowiadania na zapytanie. Załóżmy, że podczas tworzenia kubełków dla każdego indeksu zapamiętaliśmy jego pozycję w kubełkach. Ponadto, dodając indeks do lewego kubełka zapamiętaliśmy, oprócz owego indeksu, również aktualny rozmiar prawego kubełka (i analogicznie dodając indeks do prawego kubełka). Oczywiście znalezienie przedziału w największym kubełku jest trywialne. Jeżeli teraz pierwszy element przedziału podczas podziału powędrował do lewego kubełka, a my odpowiadając na zapytanie również chcemy zejść do lewego kubełka, to pierwszy element przedziału nie zmienia się (analogicznie dla ostatniego elementu oraz prawego kubełka)! Możemy odczytać jego pozycję w nowym kubełku z obliczonej wcześniej tablicy wszystkich pozycji wszystkich elementów. Jeżeli jednak pierwszy element powędrował do lewego kubełka, a my chcielibyśmy przejść do prawego kubełka, pierwszy element przedziału zmienia się. Zastanówmy się, czy nowy pierwszy element przedziału może być mniejszy (co do wartości indeksu) od starego. Okazuje się, że nie - w przeciwnym wypadku bowiem istniałby w przedziale element mniejszy (co do wartości indeksu) od starego początku, a zatem początek nie byby wcale początkiem. Dlatgo nowym początkiem będzie pierwszy element z prawego kubełka większy (co do wartości indeksu) od starego początku. Zatem nowy początek będzie znajdował się na pozycji, która była rozmiarem prawego kubełka w momencie, kiedy stary początek wędrował do lewego kubełka - tą wartość zaś zapamiętaliśmy! Analogiczne rozumowanie można przeprowadzić dla ostatniego elementu przedziału oraz zamieniając prawy i lewy kubełek miejscami. Umiemy zatem mając przedział w większym kubełku znaleźć w czasie stałym przedział w mniejszym kubełku. W ten sposób zredukowaliśmy czas trwania zapytania do O(log n) Okazuje się, że lepszej złożoności czasowej nie można uzyskać. Cały algorytm działa w czasie O(n log n + q log n). Załóżmy, że wykonalibyśmy n zapytań - o zerowy, pierwszy, drugi element i tak dalej. W ten sposób posortowalibyśmy nasze etykiety. Koszt takiej operacji wynosiłby O(n log n) (podstawiliśmy q = n). Okazuje się, że jeżeli jedynie porównujemy etykiety między sobą (a nie korzystamy z tego, że są liczbami całkowitymi na przykład), jest to najlepsza możliwa do uzyskania złożoność. Zachęcamy do zmierzenia się z implementacją przedstawionych algorytmów w zadaniach: Query on a tree III, Mediana, Pre-order, któych treści znajdziesz na następnej stronie. Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




