Query on a tree III
19.02.2010 - Wiktor Janas
    Na szczęście nie. Uratuje nas fakt, że wprawdzie etykiety są duże, ale jest ich niewiele (przynajmniej nie więcej niż wierzchołków drzewa). Możemy zatem stworzyć izomorfizm miedzy etykietami a liczbami z zakresu 1 ... n (gdzie n jest ilością możliwych etykiet). Kluczową obserwacją jest to, że nie interesuje nas wartość etykiety (na przykład 214.042), a jedynie jej pozycja względem innych etykiet (czyli 214.042 < 324.441). Spróbujmy przenumerować etykiety tak, aby relacja mniejszości została zachowana, a liczby, którymi operujemy, były mniejsze. W tym celu wystarczy na początku programu posortować wszystkie etykiety. Następnie najmniejszą etykietę zamienić na 1, kolejną na 2, następną na 3 i tak dalej. Jeżeli będziemy jedynie porównywać etykiety między sobą, nigdy nie zorientujemy się, co się stało. Koszt całej maskarady to tylko O(n log n) na początku programu, a zatem całkiem nieźle. 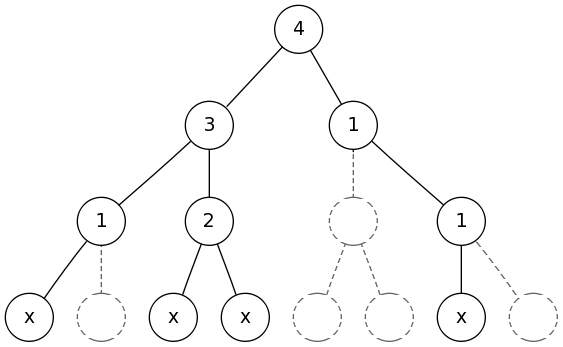
Przyjrzyjmy się jeszcze rozmiarowi drzewa licznikowego. Będzie ono miało n liści, zatem wszystkich wierzchołków 2n-1. Przypomnijmy algorytm: rozpatrując wierzchołek v, tworzymy zbiory wierzchołków dla wszystkich poddrzew, każdy taki zbiór reprezentując jako drzewo licznikowe. Niestety poddrzew tych może być dużo (nawet rzędu n), zatem złożoność pamięciowa tego kroku byłaby O(n · (2n-1)) – za dużo. Chcielibyśmy, aby drzewo licznikowe zużywało pamięć tylko, kiedy jest to rzeczywiście niezbędne, czyli aby jego rozmiar rósł proporcjonalnie względem ilości elementów, które przechowuje. Suma mocy poddrzew nigdy nie przekroczy ilości wierzchołków w całym drzewie, zatem suma rozmiarów drzew licznikowych również byłaby pod kontrolą. Po połączeniu drzew licznikowych moglibyśmy usunąć oryginały (nie będą już potrzebne), dzięki czemu ilość zużywanej pamięci w każdym momencie byłaby O(n). Rzeczywiście można zaimplementować takie "pływające" drzewo licznikowe. Idea polega na tym, aby nie tworzyć wszystkich wierzchołków i liści na starcie, lecz w miarę dodawania nowych elementów. Zauważmy, że nie przeczy to pomysłowi zarezerwowania każdemu możliwemu elementowi miejsca w drzewie. Doskonale wiemy, gdzie ma wylądować każdy element – po prostu nie alokujemy dla niego pamięci, dopóki nie jest ona potrzebna, czyli pamiętamy tylko tą istotną (niepustą) część drzewa. Rysunek obok przedstawia drzewo licznikowe poprzedniego przykładu w wersji "pływającej". Linią przerywaną zaznaczono wierzchołki, dla których nie rezerwujemy pamięci. 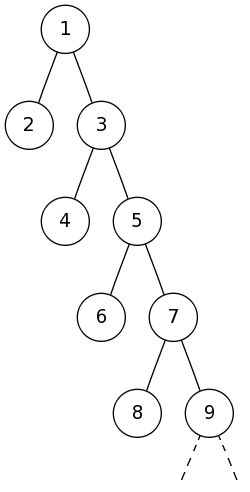
Ostatnią trudnością jest sposób łączenia drzew licznikowych. Łatwo jest w czasie liniowym wyciągnąć wszystkie elementy drzewa licznikowego. Gdybyśmy jednak utworzyli nowe drzewo licznikowe i wrzucali do niego kolejne znajdowane elementy ze wszystkich poddrzew, ilość wykonywanych operacji byłaby zbyt duża (na przykład dla drzewa na rysunku obok). Na szczęście nie musimy tworzyć nowego drzewa licznikowego. Zamiast tego będziemy sklejać dwa drzewa kopiując elementy z mniejszego do większego (rozmiary drzew znamy – są zapisane w korzeniach). Następnie mniejsze drzewo wyrzucimy, a większe drzewo połączymy z kolejnym w ten sam sposób. Dzięki temu jeden element będzie kopiowany do nowego drzewa co najwyżej log n razy (prześledź losy jednego elementu i zastanów się, jak zmieniają się rozmiary drzewa, w którym się znajduje), zatem ilość wszystkich operacji, jakie wykonamy odpowiadając na wszystkie zapytania będzie O(n log n log n) (pamiętamy, że dodawanie elementu do drzewa licznikowego trwa O(log n); zauważ, że złożoność opisanego algorytmu nie zależy od ilości zapytań). W ten sposób otrzymujemy rozwiązanie o złożoności czasowej O(n log2n + q log n) oraz liniowej złożoności pamięciowej. Jest ono niestety dość skomplikowane i raczej nieprzyjemne w implementacji. W dalszej części przedstawimy rozwiązanie zdecydowanie ciekawsze. Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




