Kolory i kompresja
20.04.2010 - Krzysztof Dryś
  Kompresja bezstratna - prosty przykład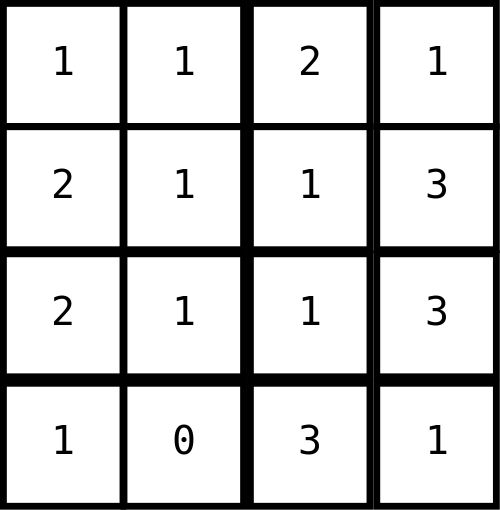 Schematyczny obrazek, który chcemy zapisać. Liczba oznacza jasność danego piksela. Wszystkie liczby są z przedziału [0,3], dlatego, że jasność każdego piksela pamiętamy na dwóch bitach.
Schematyczny obrazek, który chcemy zapisać. Liczba oznacza jasność danego piksela. Wszystkie liczby są z przedziału [0,3], dlatego, że jasność każdego piksela pamiętamy na dwóch bitach.
Wyobraźmy sobie, że mamy do zapisania czarno-biały obrazek o wielkości 4 na 4 piksele. Wartość każdego piksela pamiętana jest na 2 bitach. Zapisywać naiwnie, to zapisywać:
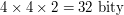 . .
Spróbujmy zrobić to inaczej. Spróbujmy zapisać:
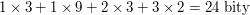 . W ten sposób oszczędziliśmy 8 bitów. To nie za dużo, prawda? Ale pamiętajmy, że nasz obrazek był naprawdę mały (4 na 4 piksele), a każdy piksel był pamiętany tylko na 2 bitach. Lepiej myśleć, że udało się nam oszczędzić jedną czwartą miejsca - jeżeli nasz wyjściowy obrazek byłbym duży, to byłoby to naprawdę sporo. . W ten sposób oszczędziliśmy 8 bitów. To nie za dużo, prawda? Ale pamiętajmy, że nasz obrazek był naprawdę mały (4 na 4 piksele), a każdy piksel był pamiętany tylko na 2 bitach. Lepiej myśleć, że udało się nam oszczędzić jedną czwartą miejsca - jeżeli nasz wyjściowy obrazek byłbym duży, to byłoby to naprawdę sporo.
Oczywiście powyższy przykład jest trochę sztuczny. Zapisując ten obrazek musielibyśmy umieścić gdzieś informacje o tym, jak kodujemy (pamiętamy) poszczególne liczby. Ale widać na nim ogólną zasadę: wykorzystaliśmy to, że jedne wartości są dużo częstsze od innych. Na tym właśnie polega kompresja bezstratna - na szukaniu zależności na obrazku. (1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




