Kolory i kompresja
20.04.2010 - Krzysztof Dryś
  Czy uważaliście na biologii?Człowiek tak na prawdę widzi tylko trzy kolory: czerwony, zielony i niebieski. Właśnie dlatego obrazek zapisujemy jako trzy macierze R,G i B - jest to sposób dla nas najbardziej naturalny. Jak sami się przed chwilą przekonaliśmy, spośród tych trzech kolorów najlepiej rozróżniamy zielony. Wytłumaczyć to można (nie do końca na poważnie) tym, że ludzie pierwotni większą część swojego czas spędzali w lasach. I dlatego musieli dobrze rozpoznawać rośliny oraz kryjące się między nimi zwierzęta. Jeżeli uważaliście na biologii to wiecie, że w ludzkim oku znajdują się pręciki i czopki. Pierwsze odpowiadają za za widzenie czarno-białe, drugie za widzenie barwne. Pręcików jest dużo więcej i są dużo czulsze. To między innymi dlatego, gdy jest ciemno, nie widzimy kolorów.
No dobrze, ale co to właściwie ma wspólnego z kompresją obrazków? Możemy wykorzystać to, że lepiej rozpoznajemy jasność obiektów niż ich kolor. W tym celu wprowadzimy nową reprezentację obrazków. Do tej pory trzy macierze R,G i B mówiły ile jest poszczególnych kolorów w pikselach. Teraz, zamiast tego, będzie posługiwali się macierzami Jasność piksela
W tym wypadku trudniej będzie o łatwą i ładną interpretację tego, co te macierze zawierają. Pierwsza z nich, macierz
Czy ten wzór jest ciekawy? Zdecydowanie! Przede wszystkim, jest kolejnym potwierdzeniem faktu, który my już przed chwilą zauważyliśmy: nie ma równości między kolorami. Zauważmy bowiem, że współczynniki przy czerwonym, zielonym i niebieskim są różne. Oznacza to, że zielony piksel wydaje się nam jaśniejszy od niebieskiego piksela. Najlepiej zobaczyć to na przykładzie:  Powyżej widzimy trzy (czyste) kolory. Najjaśniejszy wydaje się zielony, a najciemniejszy niebieski.
Powyżej widzimy trzy (czyste) kolory. Najjaśniejszy wydaje się zielony, a najciemniejszy niebieski.
Macierz
To nie są dokładne wzory! Ale dokładne wzory nie są zbyt ciekawe. A my chyba mamy już na dzisiaj dosyć cyferek, prawda? Gdyby ktoś jednak chciał dokładniej poznać podział na składowe YCrCb, to może skorzystać z
artykułu na Wikipedii.
No dobrze, ale po co nam tak właściwie te macierze? I jaki ma to związek z kompresją? Jesteśmy już coraz bliżej odpowiedzi na to pytanie. Najpierw popatrzmy na rozkład naszego obrazka na składowe Y,Cr i Cb:
Gdy rozkładaliśmy obrazek na składowe R,G i B to wszystkie kanały były (do pewnego stopnia) czarno-białą wersją oryginału. Tym razem już tak nie jest. Tylko składowa Dla nas jest to świetna wiadomość. Oznacza ona, że możemy pozwolić sobie na stratną kompresję składowych chromatycznych, bo i tak niewiele one wnoszą do naszego obrazka. Sprytniejszy algorytm kompresjiPopatrzmy na poniższy algorytm:
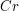 i i 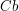 , to zazwyczaj będziemy stosowali nasz algorytm z parametrem , to zazwyczaj będziemy stosowali nasz algorytm z parametrem  mniejszym od parametrów mniejszym od parametrów 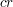 i i 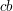 . .
Cała ta teoria brzmi mądrze. Ale najlepiej od razu sprawdzić, jak nasz algorytm zachowuje się w praktyce. W tym celu uruchomimy go dla różnych zestawów parametrów (y,cr,cb).  Wynik działania algorytmu z parametrami (y=4,cr=1,cb=1). To znaczy: dla warstwy jasności pamiętamy jedynie średnie kwadratów o boku 4. Dla warstw chromatycznych pamiętamy wszystkie piksele.
Wynik działania algorytmu z parametrami (y=4,cr=1,cb=1). To znaczy: dla warstwy jasności pamiętamy jedynie średnie kwadratów o boku 4. Dla warstw chromatycznych pamiętamy wszystkie piksele.
 Wynik działania algorytmu z parametrami (y=16,cr=1,cb=1). To znaczy: dla warstwy jasności pamiętamy jedynie średnie kwadratów o boku 4. Dla warstw chromatycznych pamiętamy wszystkie piksele.
Wynik działania algorytmu z parametrami (y=16,cr=1,cb=1). To znaczy: dla warstwy jasności pamiętamy jedynie średnie kwadratów o boku 4. Dla warstw chromatycznych pamiętamy wszystkie piksele.
 Wynik działania algorytmu z parametrami (y=1,cr=4,cb=4). To znaczy: dla warstw chromatycznych pamiętamy jedynie średnie kwadratów o boku 4. Dla warstwy jasności pamiętamy wszystkie piksele.
Wynik działania algorytmu z parametrami (y=1,cr=4,cb=4). To znaczy: dla warstw chromatycznych pamiętamy jedynie średnie kwadratów o boku 4. Dla warstwy jasności pamiętamy wszystkie piksele.
 Wynik działania algorytmu z parametrami (y=1,cr=16,cb=16). To znaczy: dla warstw chromatycznych pamiętamy jedynie średnie kwadratów o boku 16. Dla warstwy jasności pamiętamy wszystkie piksele.
Wynik działania algorytmu z parametrami (y=1,cr=16,cb=16). To znaczy: dla warstw chromatycznych pamiętamy jedynie średnie kwadratów o boku 16. Dla warstwy jasności pamiętamy wszystkie piksele.
Te obrazki są dowodem na to, że składowa Y jest dużo ważniejsza od składowych Cr i Cb. Przy zastosowaniu parametrów (1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


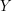 ,
, ![$$ Y[i,j] = 0.299 \cdot R[i,j] + 0.587 \cdot G[i,j] + 0.114 \cdot B[i,j]$$](/files/tex/cf36ba263ab5b195745b0881f50ba850796bb4c8.png)
![$ Cr[i,j] \approx R[i,j] - Y[i,j] $](/files/tex/c919c945ce7999ec4b5cede09ff9ef192109ede7.png)
![$ Cb[i,j] \approx B[i,j] - Y[i,j] $](/files/tex/5c1b3e6758f535b76fb02ace73426bad0bec5016.png)



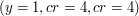 prawie nie widać różnicy względem orginalnego obrazka. Przy zestawie
prawie nie widać różnicy względem orginalnego obrazka. Przy zestawie 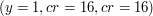 widać trochę przebarwień, szczególnie na krawędziach. Ale ogólne wrażenie jest raczej pozytywne. Natomiast przy zestawie
widać trochę przebarwień, szczególnie na krawędziach. Ale ogólne wrażenie jest raczej pozytywne. Natomiast przy zestawie 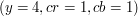 obrazek staje się zamazany i niewyraźny. Wreszcie zestaw
obrazek staje się zamazany i niewyraźny. Wreszcie zestaw 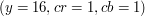 powoduje, że na obrazku ciężko coś zobaczyć.
powoduje, że na obrazku ciężko coś zobaczyć.


