Kolory i kompresja
20.04.2010 - Krzysztof Dryś
  Kompresja stratna, czyli czarna magia oraz magii owej całkowite zdemaskowanieDo tej pory nikt nas jeszcze nie oszukał. Nareszcie przyszedł na to czas. Kompresja stratna, jak sama nazwa wskazuje, osiąga zmniejszenie rozmiarów obrazka przez utratę części informacji o nim. I to w taki sposób, żebyśmy tego nie zauważyli. Jak można to osiągnąć? Najpierw popatrzmy na bardzo naiwny [i kiepsko działający!] algorytm kompresji stratnej.
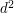 . Dla . Dla 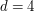 daje nam to 16 krotną kompresję! A gdzie są straty? W tym samym miejscu: tracimy informację o poszczególnych pikselach, a pamiętamy tylko średnie. daje nam to 16 krotną kompresję! A gdzie są straty? W tym samym miejscu: tracimy informację o poszczególnych pikselach, a pamiętamy tylko średnie.


 Oryginalny obrazek oraz dwie jego wersje po zastosowaniu naiwnego algorytmu kompresującego stratnie. Po środku wersja z parametrem d=4, po prawej d=8. Z pozoru tylko prawy obrazek mocno odbiega od pierwowzoru. Warto jednak kliknąć na środkowy obrazek, żeby go powiększyć i zobaczyć, że i jemu nie posłużyła kompresja stratna.
Oryginalny obrazek oraz dwie jego wersje po zastosowaniu naiwnego algorytmu kompresującego stratnie. Po środku wersja z parametrem d=4, po prawej d=8. Z pozoru tylko prawy obrazek mocno odbiega od pierwowzoru. Warto jednak kliknąć na środkowy obrazek, żeby go powiększyć i zobaczyć, że i jemu nie posłużyła kompresja stratna.
Czas na koloryTen artykuł miał być o kolorach, a my póki co mówimy tylko o obrazkach czarno-białych. Najwyższy czas to zmienić. Najpierw przekształcimy poprzedni algorytm na taki, który działa dla kolorowych obrazków.
No dobrze, ale co w tym ciekawego? Popatrzmy na wyniki działania tego algorytmu dla trzech różnych parametrów:  Wynik działania algorytmu z parametrami (r=16,g=1,b=1). To znaczy: dla czerwonej warstwy pamiętamy jedynie średnie kwadratów o boku 16. Dla pozostałych warstw pamiętamy wszystkie piksele. Widać trochę przebarwień, szczególnie w okolicach gór.
Wynik działania algorytmu z parametrami (r=16,g=1,b=1). To znaczy: dla czerwonej warstwy pamiętamy jedynie średnie kwadratów o boku 16. Dla pozostałych warstw pamiętamy wszystkie piksele. Widać trochę przebarwień, szczególnie w okolicach gór.
 Wynik działania algorytmu z parametrami (r=1,g=16,b=1). To znaczy: dla zielonej warstwy pamiętamy jedynie średnie kwadratów o boku 16. Dla pozostałych warstw pamiętamy wszystkie piksele. Widać wyraźne różnice w stosunku do oryginału. Szczególnie rzuca się w oczy kwadratowy wzorek widoczny na obrazku.
Wynik działania algorytmu z parametrami (r=1,g=16,b=1). To znaczy: dla zielonej warstwy pamiętamy jedynie średnie kwadratów o boku 16. Dla pozostałych warstw pamiętamy wszystkie piksele. Widać wyraźne różnice w stosunku do oryginału. Szczególnie rzuca się w oczy kwadratowy wzorek widoczny na obrazku.
 Wynik działania algorytmu z parametrami (r=16,g=1,b=16). To znaczy: dla niebieskiej warstwy pamiętamy jedynie średnie kwadratów o boku 16. Obrazek jest bardzo zbliżony do oryginału. Przebarwienia widać głównie na styku gór i nieba.
Wynik działania algorytmu z parametrami (r=16,g=1,b=16). To znaczy: dla niebieskiej warstwy pamiętamy jedynie średnie kwadratów o boku 16. Obrazek jest bardzo zbliżony do oryginału. Przebarwienia widać głównie na styku gór i nieba.
Żądamy równości dla kolorów!Czy spodziewaliście się, że algorytm da różne rezultaty w zależności od tego, którą warstwę przeznaczymy do kompresji? Okazało się bowiem, że w pewnym sensie warstwa zawierająca informację o kolorze zielonym jest najważniejsza. Stratne kompresowanie jej jest najbardziej widoczne. Natomiast zmiany w warstwie czerwonej i niebieskiej są już dużo trudniej zauważalne. (1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




