Kolory i kompresja
20.04.2010 - Krzysztof Dryś
  Jeżeli nie widać różnicy, to po co przepłacać?
Zobaczmy jakie oszczędności daje nam zastosowanie naszego algorytmu. Załóżmy, że stosujemy zestaw paremtrów Algorytm, który przed chwilą zobaczyliśmy jest częścia standardu kompresji JPEG. Jest on wykorzystywany w jednym z najbardziej popularnym rodzaju plików - jpg. To co zobaczyliśmy jest tylko początkiem tego algorytmu kompresji. Następnym jego krokiem jest (uwaga, trudna nazwa!) dyskretna transformata cosinusowa. Niestety, żeby ją zrozumieć, trzeba wiedzieć trochę o algebrze liniowej i analizie matematycznej. Jednak jej istota jest bardzo podobna: polega ona na podzieleniu obrazka na części ważniejsze i mniej ważne, a następnie na zapomnieniu (przynajmniej w części) o części mniej ważnej. W ten sposób wykorzystaliśmy to, że składowe chromatyczne są mniej ważne zatem możemy je kompresować stratnie bez utraty jakosci wyjściowego obrazka. Po raz kolejny przekonaliśmy się jak łatwo oszukać nasze oczy. I po raz kolejny jest to z zyskiem dla nas. Dzięki temu możemy bowiem skutecznie oszczędzać miejsce na naszych twardych dyskach! Zdjęcie, które zostało wykorzystane w artykule pochodzi z wikipedii. Samo zdjęcie, oraz informacje o licencji na jakiej jest rozpowszechniane można znaleźć na tej stronie.
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


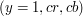 . Oznacza to, że warstwy Cr i Cb zmniejszą sie odpowiednio
. Oznacza to, że warstwy Cr i Cb zmniejszą sie odpowiednio 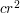 i
i 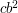 razy. Gdybyśmy chcieli zapisywać nasz obrazek naiwnie, to przy zastosowaniu
razy. Gdybyśmy chcieli zapisywać nasz obrazek naiwnie, to przy zastosowaniu 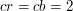 zamiast
zamiast 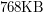 zużylibyśmy tylko
zużylibyśmy tylko 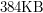 . Dla parametrów
. Dla parametrów 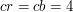 dostalibyśmy tylko
dostalibyśmy tylko 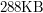 . Ogólnie, po zastosowaniu kompresji z dowolnymi parametrami cr i cb nasz obrazek zmniejszyłby się
. Ogólnie, po zastosowaniu kompresji z dowolnymi parametrami cr i cb nasz obrazek zmniejszyłby się 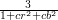 razy..
razy..


