Liczenie po chińsku ...okiem programisty

W poprzedniej części artykułu udało nam się rozwiązać zadanie o defiladzie policjantów. Czy przypominasz sobie, jaką metodą rozwiązywaliśmy tamtą zagadkę? Teraz postaramy się zrobić to szybciej i lepiej. Dlaczego? Poniższe zadanie jest bardzo podobne do Wrocławskich policjantów, ale danych jest więcej (choć nie wszystkie są istotne).

Wyspa zagadkowa(*) eksportuje znakomite owoce, spotykane tylko na Wyspie. Pewnego dnia w pakowalni owoców zaszedł interesujący wypadek. Gdy chciano pakować owoce w paczki po 10 sztuk (w każdą paczkę pakowano zawsze tę samą liczbę owoców), zostawało ich 9, gdy pakowano po 9,  to zostawało po 8, gdy pakowano po 8, to zostawało 7. Próbowano pakować coraz mniejszą liczbę owoców do jednej paczki, lecz zawsze zostawało o jeden mniej niż znajdowało się w paczce. Gdy próbowano wreszcie pakować po dwa owoce, został jeden.
Ile owoców przeznaczonych było do wysyłki na eksport?

Żeby je rozwiązać "starą" metodą wykreślania, musielibyśmy sprawdzać wszystkie liczby od do 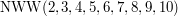. Ta ostatnia liczba nie należy do małych. Wynosi ona 2520. Jeśli najmniejszą wspólną wielokrotnością k danych jest N, to złożoność pamięciowa to także 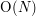, zaś czasowa.

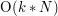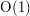Drobna modyfikacja pozwala uzyskać poprawę złożoności pamięciowej do - zamiast wykreślać liczby z tabelki po prostu sprawdzamy dla każdej wartości między 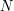a reszty z dzielenia. Nadal jednak musimy (pesymistycznie) sprawdzać reszt dla każdej z możliwości. Nawet dla małych danych wejściowych, może być bardzo dużą liczbą.

Jak policzyć to szybciej? O tym za chwilę. Na razie powiedzmy trochę więcej o tej ciekawej własności liczb, mówiącej, że rozwiązanie naszej zagadki istnieje. Nazwaliśmy ją ostatnio chińskim twierdzeniem o resztach. Brzmi ona tak:

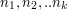Niech będą liczbami naturalnymi dodatnimi. Jeśli są one parami względnie pierwsze (będziemy to oznaczać, dla danych 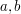:  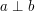), to dla dowolnych 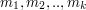istnieje dokładnie jedna liczba naturalna 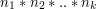mniejsza od taka, że spełnione są równania modulo(**):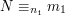

          ...

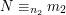
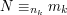
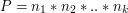Dowód przebiega podobnie, jak gdy pokazywaliśmy, że zadanie o policjantach ma jedno rozwiązanie.

Niech . Załóżmy, że istnieją dwa rozwiązania układu równań, 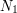i 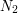, przy czym 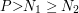. Zbadajmy liczbę 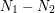. Skoro i spełniały układ równań modulo, to dla każdego :
         
         
         
         
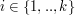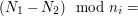
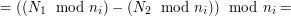
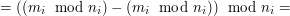
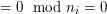
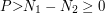Co z tego wynika? Wiemy, że . W takim razie szukamy pewnej liczby z przedziału 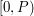takiej, że dzieli się bez reszty przez 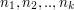. Najmniejsza taka liczba dodatnia, znana jako najmniejsza wspólna wielokrotność, jest, dla liczb parami względnie pierwszych, równa ich iloczynowi. A zatem 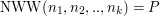. To za dużo - w takim razie jedyną możliwą wartością jest , czyli 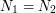. Rozwiązanie układu równań jest dokładnie jedno.

(*) Zadanie pochodzi z książki „Łamigłówki logiczne, tom 1” autorstwa L. Bogusza, P. Zarzyckiego i J. Zielińskiego

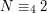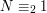(**) Oczywiście pod warunkiem, że taki układ nie jest sprzeczny. Na przykład układ: , nie ma rozwiązania.