Liczenie po chińsku ...okiem programisty
17.08.2009 - Agata Murawska
  Wiedząc już, co tak na prawdę chcemy i możemy obliczyć, możemy wrócić do szybszego algorytmu.
Zajmiemy się teraz sumą
Wszystkie składniki sumy, poza jednym, są zerami. W takim razie dla ustalonego
Jeśli przypomnimy sobie teraz, jakie warunki miał spełniać układ równań, okazuje się, że właśnie ta suma jest jego rozwiązaniem. Powiedzmy to wyraźnie:
(2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


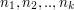 są parami względnie pierwsze i
są parami względnie pierwsze i 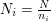 (czyli
(czyli 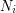 jest iloczynem
jest iloczynem 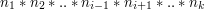 ), to
), to 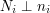 , bo
, bo 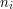 jest względnie pierwsze z każdym z czynników iloczynu
jest względnie pierwsze z każdym z czynników iloczynu 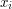 i
i 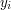 , że:
, że:
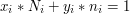
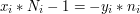
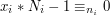
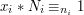
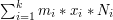 . Dla ustalonego
. Dla ustalonego  , ile wynosi reszta z dzielenia tej sumy przez
, ile wynosi reszta z dzielenia tej sumy przez 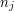 ? Policzmy wartości kolejnych składników sumy.
? Policzmy wartości kolejnych składników sumy.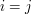 , wtedy skoro
, wtedy skoro 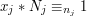 , to
, to 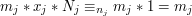
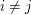 , wówczas
, wówczas 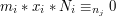 , bo
, bo 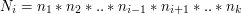 , zatem
, zatem