Co dalej? Do implementacji konieczna jest znajomość rozszerzonego algorytmu Euklidesa. Zwykły algorytm Euklidesa pozwala sprawdzić, jaki jest największy wspólny dzielnik dwóch liczb. Rozszerzona wersja daje nam znacznie więcej - dla danych  i
i  takich, że
takich, że 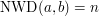 znajduje on
znajduje on  i
i  takie, ze
takie, ze 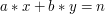 . Szczegółowe dowody poprawności i własności algorytmu nie są nam w tej chwili potrzebne, wystarczy jedynie wiedzieć, że jest to idealny sposób na znalezienie wszystkich
. Szczegółowe dowody poprawności i własności algorytmu nie są nam w tej chwili potrzebne, wystarczy jedynie wiedzieć, że jest to idealny sposób na znalezienie wszystkich 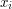 z naszych wcześniejszych rozważań.
z naszych wcześniejszych rozważań.
1
2
3
4
5
6
7
8
9
10
| int ext_Euclid(int a, int b, long long &l, long long &k){
if (!a){
l = 0;
k = 1;
return b;
}
int d = ext_Euclid(b%a, a, k ,l);
l -= (b/a)*k;
return d;
} |
Zastanówmy się na koniec, o ile udało nam się przyspieszyć znajdowanie rozwiązania. Musimy uwierzyć na słowo, że procedura ext_Euclid działa w czasie 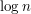 . Wykonujemy ją k razy, zatem ostateczny koszt czasowy to
. Wykonujemy ją k razy, zatem ostateczny koszt czasowy to 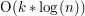 .
.
Zadania sprawdzające
- W przytoczonej na wstępie zagadce nie wszystkie dane są nam potrzebne do rozwiązania. Które z nich można pominąć i dlaczego?
- Powiedzieliśmy, że jeśli
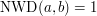 , to istnieją takie liczby
, to istnieją takie liczby  i
i  , że
, że 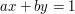 . Czy potrafisz udowodnić ten fakt?
. Czy potrafisz udowodnić ten fakt?
Wskazówka
Zastanów się nad najmniejszym elementem zbioru 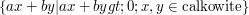 . Oznaczmy go przez
. Oznaczmy go przez 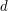 .
.
Jeśli 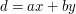 , to
, to  można przedstawić jako pewną wielokrotność
można przedstawić jako pewną wielokrotność 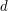 + reszta:
+ reszta: 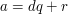 (
(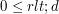 ). Spróbuj udowodnić, że
). Spróbuj udowodnić, że 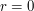 .
.




 i
i  takich, że
takich, że 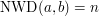 znajduje on
znajduje on  i
i  takie, ze
takie, ze 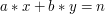 . Szczegółowe dowody poprawności i własności algorytmu nie są nam w tej chwili potrzebne, wystarczy jedynie wiedzieć, że jest to idealny sposób na znalezienie wszystkich
. Szczegółowe dowody poprawności i własności algorytmu nie są nam w tej chwili potrzebne, wystarczy jedynie wiedzieć, że jest to idealny sposób na znalezienie wszystkich 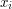 z naszych wcześniejszych rozważań.
z naszych wcześniejszych rozważań.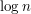 . Wykonujemy ją k razy, zatem ostateczny koszt czasowy to
. Wykonujemy ją k razy, zatem ostateczny koszt czasowy to 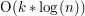 .
. 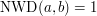 , to istnieją takie liczby
, to istnieją takie liczby 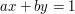 . Czy potrafisz udowodnić ten fakt?
. Czy potrafisz udowodnić ten fakt?
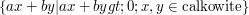 . Oznaczmy go przez
. Oznaczmy go przez 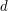 .
. 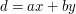 , to
, to 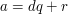 (
(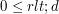 ). Spróbuj udowodnić, że
). Spróbuj udowodnić, że 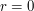 .
.


