Trie
01.12.2011 - Michał Karpiński
  Podstawową strukturą danych wykorzystywaną w algorytmach tekstowych jest drzewo trie (czyt. tri lub traj). Jest to kolejne rozwiązanie dla problemu wyszukiwania wzorca (i nie tylko). Z drzew trie korzystamy, gdy liczba zapytań jest na tyle duża, że nie opłaca się użycie klasycznych metod takich jak KMP czy BM (szczególnie gdy tekst wejściowy składa się ze sporej liczby słów). Drzewa te nadają się np. do sprawdzania poprawności pisowni. Warto dodać, że na bazie drzew trie budowane są bardziej skomplikowane struktury danych np. drzewa sufiksowe, lecz zanim zagłębimy się w zaawansowaną algorytmikę należy najpierw zrozumieć niezbędne podstawy. Jeśli pierwszy raz zetknąłeś się z problemami tekstowymi, to zapoznaj się wpierw z podstawowymi zagadnieniami i definicjami z dziedziny algorytmów tekstowych. Wróć tutaj, gdy przeczytasz ze zrozumieniem ten artykuł.Uważam, że dobrym pomysłem jest zostawienie formalnej definicji drzewa trie na później, gdyż ta struktura jest na tyle prosta, że po obejrzeniu konkretnego przykładu jej budowa okaże się bardzo intuicyjna. Na początek weźmy niewielki zbiór słów. Taki zbiór będziemy nazywać słownikiem i oznaczymy go literą 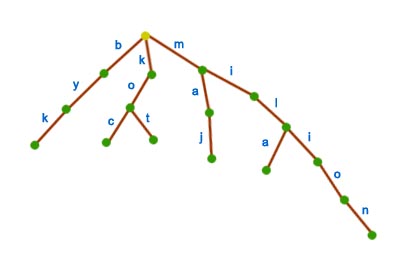 Pytanie: Czy z przedstawionego powyżej drzewa potrafimy odczytać wszystkie słowa z Po dokładnym przeanalizowaniu powyższego przykładu każdy powinien bez trudu odgadnąć sposób budowania drzew trie. Nasuwa się jednak pytanie: dlaczego reprezentować nasz słownik w taki sposób? Podstawową procedurą jaką będziemy chcieli wykonywać jest 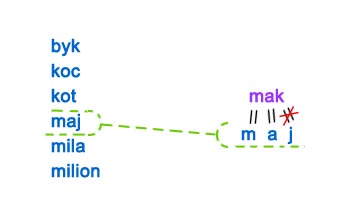 Ciekawostka: nie jest znana liczba słów w języku polskim. Źródło: link W naszym przykładzie operujemy na niewielkiej liczbie słów, więc przejście całej listy w poszukiwaniu jakiegoś słowa (np. mak, patrz rysunek powyżej) zajmuje mało czasu. Wyobraźmy sobie jednak, że jesteśmy w posiadaniu słownika o większych rozmiarach np. słownik języka polskiego. Sprawa zaczyna się nieco komplikować, nieprawdaż? Jeśli w ogólnym przypadku przyjmiemy, że Pytanie: jak będzie wyglądała procedura Przykład dla naszego słownika i 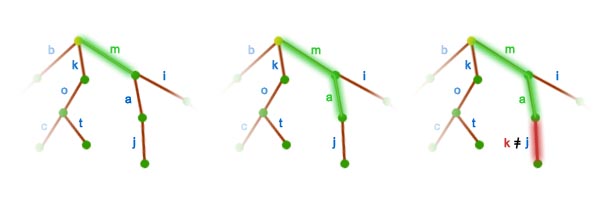 Jak się niedługo przekonamy, dzięki przeszukiwaniu drzewa trie sporo oszczędzamy na złożoności, gdyż czas zapytania jest liniowy względem długości szukanego słowa, czyli
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


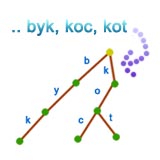
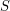 . Załóżmy, że w
. Załóżmy, że w 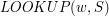 – stwierdzenie, czy słowo
– stwierdzenie, czy słowo 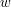 należy do słownika
należy do słownika 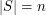 i
i 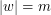 , to złożoność czasowa procedury
, to złożoność czasowa procedury 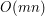 (każde z
(każde z  słów słownika porównujemy z
słów słownika porównujemy z 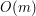 ).
).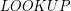 z wykorzystaniem drzewa trie (i jaką będzie miała złożoność czasową)?
z wykorzystaniem drzewa trie (i jaką będzie miała złożoność czasową)? 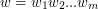 sprawdzamy, czy istnieje krawędź wychodząca z korzenia, do której przypisana jest litera
sprawdzamy, czy istnieje krawędź wychodząca z korzenia, do której przypisana jest litera 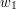 . Jeśli tak, to idziemy w dół przez tą krawędź do kolejnego wierzchołka, oznaczamy go jako aktywny i powtarzamy ten krok dla słowa
. Jeśli tak, to idziemy w dół przez tą krawędź do kolejnego wierzchołka, oznaczamy go jako aktywny i powtarzamy ten krok dla słowa 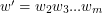 itd. Jeśli taka krawędź nie istnieje, to znaczy, że słowo nie należy do
itd. Jeśli taka krawędź nie istnieje, to znaczy, że słowo nie należy do 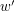 będzie słowem pustym.
będzie słowem pustym.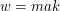 :
:

