Definicja trie
Trie jest to ukorzenione drzewo przeszukiwań przechowujące skończoną ilość kluczy (słów). Klucz jest postaci 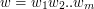 , gdzie każde
, gdzie każde 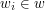 jest literą należącą do ustalonego alfabetu
jest literą należącą do ustalonego alfabetu 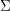 . Każdy węzeł zawiera listę krawędzi wychodzących etykietowanych literami alfabetu
. Każdy węzeł zawiera listę krawędzi wychodzących etykietowanych literami alfabetu 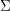 . Każdy węzeł reprezentuje pewien fragment (prefiks) klucza/y. Istnieje krawędź
. Każdy węzeł reprezentuje pewien fragment (prefiks) klucza/y. Istnieje krawędź  z węzła
z węzła  do
do  o etykiecie
o etykiecie  , jeśli prefiks klucza reprezentowanego przez
, jeśli prefiks klucza reprezentowanego przez  rozszerzony o literę
rozszerzony o literę  również jest prefiksem dla pewnego klucza (niekoniecznie tego samego).
również jest prefiksem dla pewnego klucza (niekoniecznie tego samego).
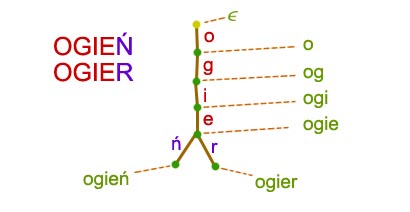
Jest to najprostsza definicja drzewa trie jaką udało mi się wymyślić. Mimo to widać, że łatwiej było wyjaśnić konstrukcję tej struktury danych na przykładzie.
Na początek przyjmiemy dwa założenia. Pierwsze: alfabet 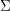 jest zbiorem skończonym np. alfabet języka polskiego (32 znaki). Będziemy się tego sztywno trzymali, gdyż w algorytmach tekstowych spotkamy się głównie z problemami związanymi z "prawdziwym tekstem", zrozumiałym dla czytelnika znającego dany język. Szczerze wątpię czy istnieją ludzie posługujący się językami nad nieskończonym alfabetem (choć pewny nie jestem :) ).
jest zbiorem skończonym np. alfabet języka polskiego (32 znaki). Będziemy się tego sztywno trzymali, gdyż w algorytmach tekstowych spotkamy się głównie z problemami związanymi z "prawdziwym tekstem", zrozumiałym dla czytelnika znającego dany język. Szczerze wątpię czy istnieją ludzie posługujący się językami nad nieskończonym alfabetem (choć pewny nie jestem :) ).
Drugie założenie: żadne słowo z 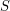 nie jest prefiksem innego słowa z
nie jest prefiksem innego słowa z 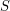 (inaczej słowa mogłyby się kończyć wewnątrz drzewa). Dzięki temu wskaźniki do każdego klucza z
(inaczej słowa mogłyby się kończyć wewnątrz drzewa). Dzięki temu wskaźniki do każdego klucza z 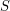 będą się znajdowały jedynie w liściach. Jest to tymczasowe założenie, którego wkrótce się pozbędziemy. Wprowadzamy je w celu uproszczenia procedur opisanych w następnej sekcji.
będą się znajdowały jedynie w liściach. Jest to tymczasowe założenie, którego wkrótce się pozbędziemy. Wprowadzamy je w celu uproszczenia procedur opisanych w następnej sekcji.
Pomocne oznaczenia:
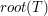 - wskaźnik na korzeń drzewa
- wskaźnik na korzeń drzewa  .
.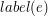 - etykieta krawędzi
- etykieta krawędzi 
Podstawowe operacje
Wyszukiwanie klucza
Wyszukiwanie przebiega zgodnie z algorytmem rekurencyjnym, którego idea została podana na poprzedniej stronie. Teraz przedstawimy tę procedurę w postaci pseudo-kodu:

Zwróćmy uwagę na wywołanie procedury. Pisząc 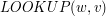 mamy na myśli komendę "sprawdź, czy słowo
mamy na myśli komendę "sprawdź, czy słowo 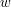 znajduje się w drzewie trie zaczynając od wierzchołka
znajduje się w drzewie trie zaczynając od wierzchołka  ". Z tego wynika, że początkowe wywołanie metody ma postać:
". Z tego wynika, że początkowe wywołanie metody ma postać: 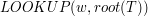 .
.
Dodawanie klucza

Dodawanie klucza do drzewa jest równie proste jak wyszukiwanie. Patrzymy na pierwszą literę słowa 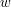 (
( 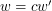 ) i sprawdzamy czy istnieje krawędź wychodząca z korzenia o etykiecie
) i sprawdzamy czy istnieje krawędź wychodząca z korzenia o etykiecie  . Jeśli istnieje taka krawędź, to wywołujemy się rekurencyjnie na wierzchołku wskazywanym przez tą krawędź dla słowa
. Jeśli istnieje taka krawędź, to wywołujemy się rekurencyjnie na wierzchołku wskazywanym przez tą krawędź dla słowa  . W przeciwnym wypadku należy utworzyć nowy wierzchołek (i krawędź o etykiecie
. W przeciwnym wypadku należy utworzyć nowy wierzchołek (i krawędź o etykiecie  ) i na nim kontynuować rekurencję. Poprawność tej metody jest oczywista.
) i na nim kontynuować rekurencję. Poprawność tej metody jest oczywista.
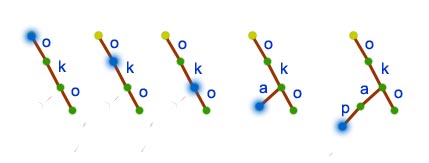 Dodanie słowa 'okap' do trie zawierającego jeden klucz: 'oko'
Dodanie słowa 'okap' do trie zawierającego jeden klucz: 'oko'
Usuwanie klucza

Żeby usunąć klucz 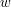 z drzewa, oczywistym jest, że
z drzewa, oczywistym jest, że 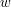 musi w tym drzewie się znajdować. Stąd pierwszym krokiem procedury
musi w tym drzewie się znajdować. Stąd pierwszym krokiem procedury 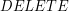 jest znalezienie liścia reprezentującego słowo
jest znalezienie liścia reprezentującego słowo 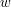 . Jeśli taki liść nie istnieje, to nie ma sensu kontynuować wykonanie algorytmu.
. Jeśli taki liść nie istnieje, to nie ma sensu kontynuować wykonanie algorytmu.
Właściwe usunięcie klucza 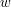 zaczynamy "od końca". Idziemy w górę drzewa i usuwamy kolejne węzły dopóki nie napotkamy węzła posiadającego przynajmniej jednego syna. Dlaczego akurat tak? poniższa symulacja usunięcia słowa gniew ze słownika {gnu, gniew} powinna wyjaśnić wszelkie wątpliwości.
zaczynamy "od końca". Idziemy w górę drzewa i usuwamy kolejne węzły dopóki nie napotkamy węzła posiadającego przynajmniej jednego syna. Dlaczego akurat tak? poniższa symulacja usunięcia słowa gniew ze słownika {gnu, gniew} powinna wyjaśnić wszelkie wątpliwości.
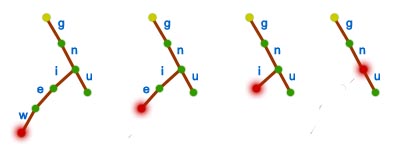
Z powyższego rysunku łatwo wywnioskować, że możemy usunąć tylko węzły, które nie są częścią innego klucza niż ten, który usuwamy.
Złożoność obliczeniowa podstawowych operacji
Analiza czasu działania przedstawionych powyżej procedur będzie się opierała na jednej ważnej obserwacji:
Liczba krawędzi wychodzących z dowolnego węzła w drzewie trie jest nie większa niż liczba liter w alfabecie 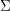 .
.
Ta obserwacja jest prawdziwa, gdyż drzewo trie jest skonstruowane tak, żeby z dowolnego węzła nie wychodziły żadne dwie krawędzie o tej samej etykiecie.
Łącząc powyższą obserwację i nasze wcześniejsze założenie o rozmiarze alfabetu można wywnioskować, że:
Jeśli 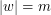 , to czas działania procedur
, to czas działania procedur 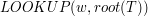 ,
, 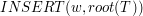 i
i 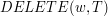 wynosi
wynosi 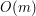 .
.
Dowód: wywołań rekurencyjnych w 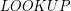 i
i 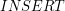 jest co najwyżej
jest co najwyżej  . Czas spędzony na przejście po liście krawędzi dla dowolnego wierzchołka wynosi
. Czas spędzony na przejście po liście krawędzi dla dowolnego wierzchołka wynosi 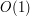 , co kończy dowód dla tych dwóch procedur.
, co kończy dowód dla tych dwóch procedur.
W procedurze 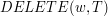 znalezienie liścia reprezentującego słowo
znalezienie liścia reprezentującego słowo 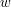 jest jednoznaczne z wywołaniem metody
jest jednoznaczne z wywołaniem metody 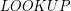 . Czas tego kroku to
. Czas tego kroku to 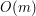 . Liczba usuniętych węzłów nie przekracza
. Liczba usuniętych węzłów nie przekracza  . Daje nam to górne ograniczenie na liczbę przebiegów pętli wewnątrz metody
. Daje nam to górne ograniczenie na liczbę przebiegów pętli wewnątrz metody 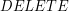 , co kończy dowód.
, co kończy dowód.










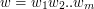 , gdzie każde
, gdzie każde 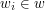 jest literą należącą do ustalonego alfabetu
jest literą należącą do ustalonego alfabetu 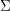 . Każdy węzeł zawiera listę krawędzi wychodzących etykietowanych literami alfabetu
. Każdy węzeł zawiera listę krawędzi wychodzących etykietowanych literami alfabetu  z węzła
z węzła  do
do  o etykiecie
o etykiecie  , jeśli prefiks klucza reprezentowanego przez
, jeśli prefiks klucza reprezentowanego przez 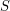 nie jest prefiksem innego słowa z
nie jest prefiksem innego słowa z 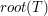 - wskaźnik na korzeń drzewa
- wskaźnik na korzeń drzewa  .
.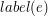 - etykieta krawędzi
- etykieta krawędzi 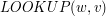 mamy na myśli komendę "sprawdź, czy słowo
mamy na myśli komendę "sprawdź, czy słowo 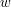 znajduje się w drzewie trie zaczynając od wierzchołka
znajduje się w drzewie trie zaczynając od wierzchołka 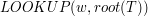 .
.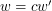 ) i sprawdzamy czy istnieje krawędź wychodząca z korzenia o etykiecie
) i sprawdzamy czy istnieje krawędź wychodząca z korzenia o etykiecie 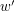 . W przeciwnym wypadku należy utworzyć nowy wierzchołek (i krawędź o etykiecie
. W przeciwnym wypadku należy utworzyć nowy wierzchołek (i krawędź o etykiecie 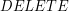 jest znalezienie liścia reprezentującego słowo
jest znalezienie liścia reprezentującego słowo 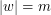 , to czas działania procedur
, to czas działania procedur 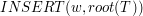 i
i 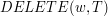 wynosi
wynosi 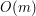 .
.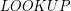 i
i 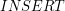 jest co najwyżej
jest co najwyżej  . Czas spędzony na przejście po liście krawędzi dla dowolnego wierzchołka wynosi
. Czas spędzony na przejście po liście krawędzi dla dowolnego wierzchołka wynosi 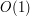 , co kończy dowód dla tych dwóch procedur.
, co kończy dowód dla tych dwóch procedur.

