Trie
01.12.2011 - Michał Karpiński
  Słowa będące prefiksami innych słówPodczas dodawania kolejnych słów do drzewa trie często się zdarza, że nowo dodane słowo jest prefiksem słowa już istniejącego w drzewie. W takich sytuacjach słowa w drzewie trie mogą się kończyć w węzłach wewnętrznych, a nie - jak wcześniej mówiliśmy - tylko w liściach. Aby nie dochodziło do niejednoznacznych sytuacji podczas wyszukiwania należy lekko zmodyfikować drzewo trie. Z każdym węzłem przechowujemy dodatkową informację o tym, czy jakieś słowo się w danym miejscu kończy. Możemy sobie wyobrazić, że jeśli w jakimś węźle kończy się słowo, to kolorujemy go na czerwono. Oczywiście wszystkie liście będą czerwone. Przykład dla słownika {pas, pal, pasmo, palto}: 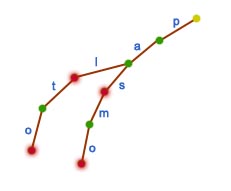 Teraz wystarczy przerobić procedury z poprzedniej strony, aby działały w ogólnym przypadku. To zadanie pozostawię czytelnikowi jako ćwiczenie. Ograniczenia drzew trieDrzewo trie jest niezwykle przydatną strukturą danych, lecz ma jedną bolesną wadę: nie jest możliwe pełne wyszukiwanie wzorca. Inaczej mówiąc - budując drzewo trie musimy mieć jasno ustalone pojęcie słowa. Weźmy przykładowe zdanie:  Słowo w zdaniu można zdefiniować jako spójny ciąg liter taki, że przed i po nim występuje znak spacji (nie licząc początku i końca zdania). W naszym przykładzie mamy sześć słów. Po zbudowaniu trie na tych słowach, będą istniały wzorce, których nie będzie można wyszukać, a będą częścią zdania. Oto przykład: 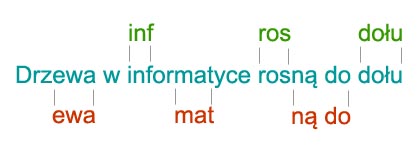 Oprócz całych słów z powodzeniem możemy wyszukiwać ich prefiksy (np. inf, ros). Jednak nie możemy szybko wyszukać wzorców, które leżą "wewnątrz" słowa (mat), są jego sufiksem (ewa) lub takich, które zawierają w sobie litery z kilku słów jednocześnie (ną do). 
Pytanie: Nie możemy nic z tym zrobić? Teraz wystarczy rozpisać wszystkie sufiksy tekstu (po prawej mamy sufiksy dla ciągu: abbaaababaabbaab). Jeśli każdy sufiks rozpatrzymy jako osobne słowo i stworzymy na nich drzewo trie, to będziemy mogli wykonywać pełne wyszukiwanie wzorca. Jaką cenę za to płacimy? Złożoność czasowa i pamięciowa konstrukcji takiego trie - przy użyciu poznanych wcześniej metod - osiąga Bardziej ambitnym czytelnikom polecam wyszukanie informacji na temat skompresowanych drzew trie, drzew sufiksowych oraz algorytmu Ukkonena. Zastosowanie drzew trie - tablica asocjacyjnaTablica asocjacyjna - zwana także tablicą skojarzeniową - jest to powszechnie stosowany abstrakcyjny typ danych, który przechowuje pary {unikalny klucz, wartość}. Dostęp do wartości możliwy jest poprzez podanie klucza. Klucz może być dowolnym typem danych (np. liczbą, pojedynczym znakiem), ale jeśli jest w postaci słowa, to naturalnym sposobem reprezentacji tablicy asocjacyjnej jest drzewo trie. Stworzenie tablicy asocjacyjnej na podstawie drzewa trie wymaga drobnej modyfikacji struktury trie. Najlepiej będzie pokazać to na przykładzie. Załóżmy, że w pewnym gospodarstwie znajduje się pewna liczba zwierząt. Nazwę zwierzęcia i liczbę w jakiej ono występuje można zapisać jako para {nazwa,liczba}:  Na nazwach zwierząt tworzymy drzewo trie. Liczby kolejnych zwierząt przechowujemy w osobnej tablicy (dynamicznej lub statycznej, w zależności od potrzeb), a w węzłach, na których kończą się słowa zapisujemy indeksy tej tablicy. Dla naszego przykładu będzie to wyglądało mniej więcej tak: 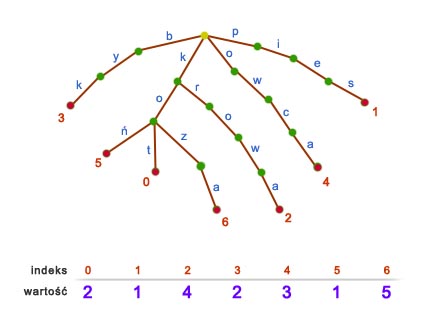 Dla przykładu czytamy: "liczba kotów znajduje się w tablicy pod indeksem 0, czyli jest ich 2 itd." (1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 występuje gdzieś w ciągu znaków
występuje gdzieś w ciągu znaków  , to
, to 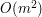 (jeśli wejściowy tekst jest rozmiaru
(jeśli wejściowy tekst jest rozmiaru  ). Istnieją pewne modyfikacje i algorytmy, które gwarantują liniowy czas konstrukcji i liniowy koszt pamięciowy, lecz są one zbyt skomplikowane, aby można było o nich mówić w dziale "Zostań zawodnikiem".
). Istnieją pewne modyfikacje i algorytmy, które gwarantują liniowy czas konstrukcji i liniowy koszt pamięciowy, lecz są one zbyt skomplikowane, aby można było o nich mówić w dziale "Zostań zawodnikiem".

