CERC 2010: Szkice rozwiązań
28.11.2010
H: Hanging HatsTreść (pdf) | wyślij rozwiązanie. Problem wymaga zaprojektowania i zaimplementowania struktury danych służącej do przechowywania zbioru S punktów płaszczyzny i wykonywania paru operacji. Aby uprościć rozwiązanie, przekształcamy problem następująco: S zawiera początkowo wszystkie zadane na wejściu punkty, a każdy z nich ma kolor czerwony. Następnie musimy wykonywać efektywnie następujące operacje:
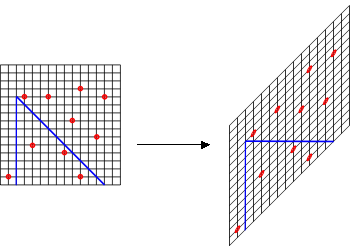
Następnie, aby rozwiązać oryginalny problem, dla każdego punktu zadanego na wejściu najpierw sprawdzamy czy należy on do S. Jeśli nie należy, wypisujemy FAIL. W przeciwnym przypadku zmieniamy jego kolor na zielony, a następnie identyfikujemy i usuwamy wszystkie punkty zawarte w jego regionie. Zauważmy, że każdy punkt będzie identyfikowany (i usuwany) co najwyżej raz, więc jeśli potrafimy identyfikować k punktów w regionie w czasie O(k log n) i usuwać pojedynczy punkt w czasie O(log n), całkowity czas działania wyniesie O(n log n). Dlatego też główną trudnością zadania jest skonstruowanie struktury pozwalającej na efektywną identyfikację punktów zawartych w regionie. Skoncentrujmy się początkowo na przypadku a=1. Aby ułatwić rozumowanie, obróćmy płaszczyznę o 135 stopni. Wtedy pytanie sprowadza się do identyfikacji punktów dominowanych przez dany punkt (x0,y0), co jest dość znanym problemem, który można rozwiązać w czasie O(k + log n). Ale wciąż musimy poradzić sobie z przypadkiem a = 2! Na szczęście nie jest on bardzo różny od przypadku a = 1: wystarczy, że poza obróceniem płaszczyzny rozciągniemy ją trochę, tak żeby interesujący nas region stał się prostokątny. Innymi słowy, istnieje liniowa transformacja, która przekształca ten problem do problemu identyfikacji punktów dominowanych Przykład takiej transformacji został przedstawiony na rysunku poniżej.
Jednak niektóre punkty mają regiony z parametrem a = 1, inne z a = 2, a transformacje dla tych dwóch przypadków są zupełnie różne! Aby poradzić sobie z tą trudnością, budujemy dwie struktury: S(1) i S(2). Obie początkowo zawierają wszystkie punkty z wejścia; S(a) pozwala na szybką identyfikację punktów zawartych w regionie ograniczonym przez proste y=a(x-x0)+y0 i y=-a(x-x0)+y0. Dodatkowo podczas usuwania punktów musimy je usuwać z obu struktur. Ostatecznie otrzymujemy całkowity czas działania O(n log n). Informacje dodatkowePoczątkującym programistom proponujemy prostszy wariant zadania w którym wszystkie kapelusze są jednego typu. Taki wariant był długo rozważany przez autorów zadań, jednak okazało się, że można go rozwiązać znacznie łatwiej. W takim przypadku wystarczy patrzeć na podstawy kapeluszy i całe zadanie sprowadza się do szybkiego sprawdzania, jakie podstawy zawierają się w danej. Początkowo rozważaliśmy też wariant, w którym kapelusze są trójwymiarowymi stożkami lub piramidami. (Tak naprawdę, nie były to kapelusze tylko wybuchające wulkany.) Okazało się to jednak niezbyt ciekawym utrudnieniem.
|
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com