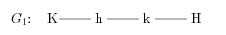CERC 2010: Szkice rozwiązań
28.11.2010
J: Justice for allTreść (pdf) | wyślij rozwiązanie. W tym zadaniu należy skonstruować graf dwudzielny, którego każda część zawiera co najwyżej k = 200 wierzchołków a liczba doskonałych skojarzeń wynosi dokładnie n. Wierzchołki w pierwszej części nazywane są rycerzami a w drugiej końmi. Pokażemy, jak skonstruować taki graf Gn, który zawiera n skojarzeń doskonałych i ma następującą dodatkową własność: ma dwa wyróżnione wierzchołki (rycerza i konia) i po ich usunięciu graf ma dokładnie jedno doskonałe skojarzenie. Skonstruowanie G1 jest bardzo proste; na rysunku poniżej K i H oznaczają wyróżnione wierzchołki.
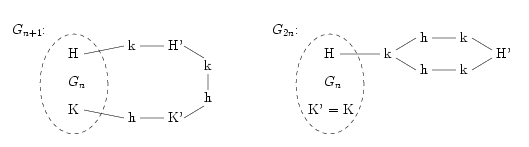
Wystarczy teraz pokazać, jak — na podstawie grafu Gn — skonstruować grafy Gn+1 i G2n. Na rysunkach poniżej K i H oznaczają wyróżnione wierzchołki grafu Gn, podczas gdy K' i H' to wyróżnione wierzchołki w nowo skonstruowanym grafie (odpowiednio w Gn+1 lub w G2n).
Sprawdzenie, że grafy te spełniają daną zależność jest prostym ćwiczeniem. Całe rozwiązanie polega na iteracyjnym konstruowaniu grafów i dojścia do zadanego grafu Gn w logarytmicznej liczbie kroków. Informacje dodatkowePodczas konstrukcji zestawu zadań uważaliśmy, że wszystkie zadania poza J są możliwe do zrobienia przez zawodników. Zadanie J miało być zadaniem, którego nie zrobi żadna drużyna (pożądany jest podobny warunek, tj. żadna drużyna nie robi wszystkich zadań, co gwarantuje, że żadna drużyna nie opuszcza zawodów przed ich końcem). Upewniliśmy się nawet, że zadanie jest odpowiednio trudne testując, jak długo zajmie jego wymyślenie naukowcowi zajmującemu się algorytmiką i skojarzeniami. Okazało się, że wymyślenie rozwiązania (gorszego niż podane powyżej) zajęło parę dni. Uznaliśmy zatem, że możemy spać spokojnie. Jakież było nasze zaskoczenie, gdy pierwsza drużyna, która rozwiązała to zadanie, zrobiła to w ciągu pierwszych 2 godzin! Implementacja zadania jest bardzo prosta. Warto jednak przypomnieć, że poprawnych wyników może być wiele i konieczny jest program weryfikujący odpowiedź. Program ten — w odróżnieniu od programu wymaganego przez zawodników — musi zliczać skojarzenia w dowolnym grafie dwudzielnym. Jest to problem #P-zupełny, co oznacza, że nie są znane algorytmy (i naukowcy mocno wierzą w to, że nie istnieją) działające w czasie wielomianowym. W szczególności opis grafu ma rozmiar k2, zaś nasz algorytm weryfikujący liczy liczbę skojarzeń w czasie O(k n).
|
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com