Najdłuższy wspólny podciąg
02.10.2010 - Marcin Oczeretko
  Zadanie A
Czy potrafisz szybko odpowiadać na wiele pytań o najdłuższy wspólny podciąg pary dowolnych prefiksów wyrazów Wejście
Pierwszy wiersz wejścia zawiera ciąg znaków (małe i duże litery alfabetu łacińskiego oraz cyfry
W wierszu drugim znajduje się ciąg liter będący słowem
Trzeci wiersz zawiera jedną liczbę naturalną
W każdej z kolejnych Wyjście
Dla każdej pary liczb PrzykładDla wejścia:
cdcddbdadbcdbdbddada Poprawnym wyjściem będzie:
dcdd
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
Zadanie BW tym zadaniu należy jedynie znaleźć długość LCS dla dwóch podanych na wejściu wyrazów. Limit pamięci jest jednakże niewielki, dlatego postaraj się ograniczyć jej zużycie. Wejście
Wejście składa się z dwóch wierszy. W każdym znajduje się niepusty ciąg znaków (małe litery alfabetu łacińskiego) o długości mniejszej niż Wyjście
Należy wypisać jedną nieujemną liczbę całkowitą równą długości najdłuższego wspólnego podciągu wyrazów PrzykładDla wejścia:
dcbbaacbda Poprawnym wyjściem będzie: 6
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
(10 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 i
i  ?
?
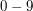 ) będący wyrazem
) będący wyrazem 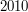 .
.
 .
.
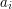 i
i 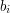 , że długość
, że długość 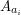 i
i 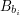 (gdzie
(gdzie 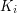 to wyraz będący
to wyraz będący  pierwszymi literkami wyrazu
pierwszymi literkami wyrazu 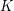 ). Jeśli istnieje wiele podciągów o największej długości, to wypisz dowolny z nich. Jeśli LCS będzie miał długość 0 (czyli będzie słowem pustym), to zamiast niego wypisz znak !.
). Jeśli istnieje wiele podciągów o największej długości, to wypisz dowolny z nich. Jeśli LCS będzie miał długość 0 (czyli będzie słowem pustym), to zamiast niego wypisz znak !.
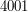 . Pierwszy wiersz zawiera wyraz
. Pierwszy wiersz zawiera wyraz 

