Odtwarzamy wygląd LCS
Wyobraźmy sobie, że w każdej komórce 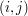 tablicy poza liczbą znajduje się też i strzałka, która wskazuje na pole zawierające tę wartość, która była nam potrzebna przy wyliczaniu liczby w
tablicy poza liczbą znajduje się też i strzałka, która wskazuje na pole zawierające tę wartość, która była nam potrzebna przy wyliczaniu liczby w 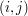 . Zauważmy, że jeśli
. Zauważmy, że jeśli ![$ A[i]=B[j] $](/files/tex/3db538d9ca4640dd8802547b0069ddc11f3a8a20.png) to strzałka w
to strzałka w 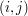 będzie skierowana na skos, a jeśli
będzie skierowana na skos, a jeśli ![$ A[i] \neq B[j] $](/files/tex/c091a466653a32786bcb3d99ab45b48869175097.png) , to w górę lub w lewo - zależnie od tego, gdzie będzie większa wartość (w przypadku remisu kierunek strzałki jest dowolny).
, to w górę lub w lewo - zależnie od tego, gdzie będzie większa wartość (w przypadku remisu kierunek strzałki jest dowolny).
Strzałka skośna odpowiada "przedłużaniu" LCS o ostatnią literkę obu rozpatrywanych prefiksów (przypadek "a" z obserwacji pierwszej).
Strzałki w lewo i w górę odpowiadają następującej decyzji: czy dłuższym podciągiem 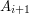 i
i 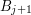 będzie LCS
będzie LCS 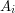 i
i 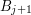 , czy może LCS
, czy może LCS 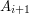 i
i 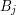 ?
?
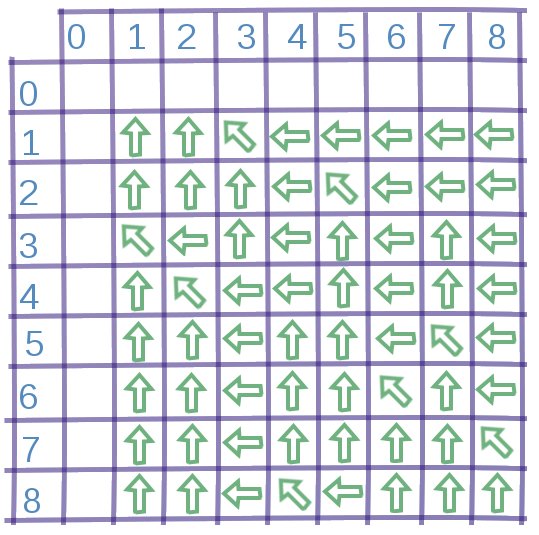 Przykładowe rozmieszczenie strzałek.
Przykładowe rozmieszczenie strzałek.
Aby odtworzyć LCS musimy przejść zgodnie ze strzałkami z pola  do lewej bądź górnej krawędzi tablicy. Za każdym razem, gdy pójdziemy na skos, znajdujemy kolejną literkę z LCS. W związku z tym, że cała tablica jest już wypełniona wartościami
do lewej bądź górnej krawędzi tablicy. Za każdym razem, gdy pójdziemy na skos, znajdujemy kolejną literkę z LCS. W związku z tym, że cała tablica jest już wypełniona wartościami  , strzałki wskazują zawsze ten wybór, który prowadzi do najdłuższego podciągu. Jeśli więc natrafimy na strzałkę skośną w polu
, strzałki wskazują zawsze ten wybór, który prowadzi do najdłuższego podciągu. Jeśli więc natrafimy na strzałkę skośną w polu 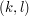 , oznacza to, że najlepiej będzie jako kolejną literkę odtwarzanego LCS wybrać
, oznacza to, że najlepiej będzie jako kolejną literkę odtwarzanego LCS wybrać ![$ A[k] = x $](/files/tex/20d0fdbe4ad43b963f0c06881f9c2c9c908c7580.png) (zachodzi też
(zachodzi też ![$ x = B[l] $](/files/tex/171efe3a5b22dc0e17a460064468c313e4bbe211.png) , bo tylko w takiej sytuacji mogliśmy natrafić na strzałkę na skos). Pamiętajmy jednak, że odtwarzamy LCS od końca!
, bo tylko w takiej sytuacji mogliśmy natrafić na strzałkę na skos). Pamiętajmy jednak, że odtwarzamy LCS od końca!
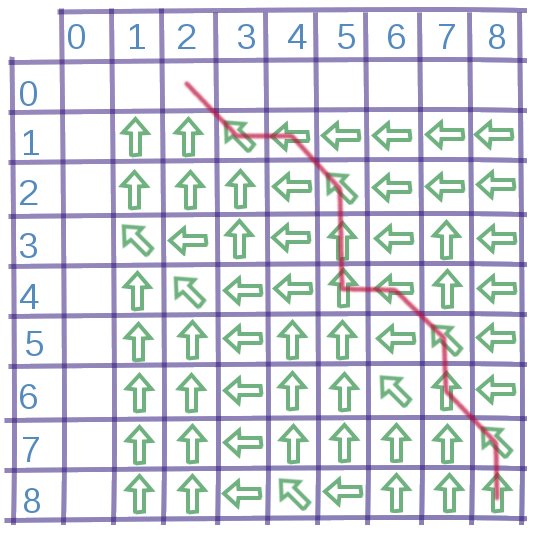 Na czerwono zaznaczona jest droga do krawędzi wyznaczona przez strzałki.
Na czerwono zaznaczona jest droga do krawędzi wyznaczona przez strzałki.
Oczywiście nie musimy uwzględniać żadnych strzałek w naszym kodzie. Wystarczy bowiem kilka porównań, aby sprawdzić w którą stroną skierowana by była strzałka w danym polu. Jeśli ![$ A[i]=B[j] $](/files/tex/3db538d9ca4640dd8802547b0069ddc11f3a8a20.png) , to w polu
, to w polu 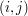 znajdowałaby się strzałka na skos. W przeciwnym wypadku musimy sprawdzić w którym z pól
znajdowałaby się strzałka na skos. W przeciwnym wypadku musimy sprawdzić w którym z pól 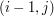 czy
czy 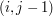 wpisana jest większa wartość - na to pole wskazywałaby strzałka z komórki
wpisana jest większa wartość - na to pole wskazywałaby strzałka z komórki 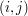 .
.






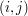 tablicy poza liczbą znajduje się też i strzałka, która wskazuje na pole zawierające tę wartość, która była nam potrzebna przy wyliczaniu liczby w
tablicy poza liczbą znajduje się też i strzałka, która wskazuje na pole zawierające tę wartość, która była nam potrzebna przy wyliczaniu liczby w ![$ A[i]=B[j] $](/files/tex/3db538d9ca4640dd8802547b0069ddc11f3a8a20.png) to strzałka w
to strzałka w ![$ A[i] \neq B[j] $](/files/tex/c091a466653a32786bcb3d99ab45b48869175097.png) , to w górę lub w lewo - zależnie od tego, gdzie będzie większa wartość (w przypadku remisu kierunek strzałki jest dowolny).
, to w górę lub w lewo - zależnie od tego, gdzie będzie większa wartość (w przypadku remisu kierunek strzałki jest dowolny).
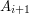 i
i 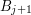 będzie LCS
będzie LCS 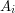 i
i 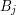 ?
?
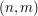 do lewej bądź górnej krawędzi tablicy. Za każdym razem, gdy pójdziemy na skos, znajdujemy kolejną literkę z LCS. W związku z tym, że cała tablica jest już wypełniona wartościami
do lewej bądź górnej krawędzi tablicy. Za każdym razem, gdy pójdziemy na skos, znajdujemy kolejną literkę z LCS. W związku z tym, że cała tablica jest już wypełniona wartościami 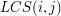 , strzałki wskazują zawsze ten wybór, który prowadzi do najdłuższego podciągu. Jeśli więc natrafimy na strzałkę skośną w polu
, strzałki wskazują zawsze ten wybór, który prowadzi do najdłuższego podciągu. Jeśli więc natrafimy na strzałkę skośną w polu 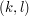 , oznacza to, że najlepiej będzie jako kolejną literkę odtwarzanego LCS wybrać
, oznacza to, że najlepiej będzie jako kolejną literkę odtwarzanego LCS wybrać ![$ A[k] = x $](/files/tex/20d0fdbe4ad43b963f0c06881f9c2c9c908c7580.png) (zachodzi też
(zachodzi też ![$ x = B[l] $](/files/tex/171efe3a5b22dc0e17a460064468c313e4bbe211.png) , bo tylko w takiej sytuacji mogliśmy natrafić na strzałkę na skos). Pamiętajmy jednak, że odtwarzamy LCS od końca!
, bo tylko w takiej sytuacji mogliśmy natrafić na strzałkę na skos). Pamiętajmy jednak, że odtwarzamy LCS od końca!
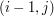 czy
czy 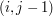 wpisana jest większa wartość - na to pole wskazywałaby strzałka z komórki
wpisana jest większa wartość - na to pole wskazywałaby strzałka z komórki 

