Najdłuższy wspólny podciąg
02.10.2010 - Marcin Oczeretko
  AlgorytmJeśli poniższy opis wyda ci się niejasny, możesz spojrzeć na szóstą stronę tego tekstu, gdzie znajduje się przykład działania algorytmu na dwóch konkretnych wyrazach.
Jeśli liczby  Przykładowa tablica, która może posłużyć do wyznaczenia LCS dla dwóch słów o długości 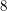 . .
Skoro prawdą jest, że  Wpisujemy zera. (10 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 i
i  są długościami odpowiednio
są długościami odpowiednio  i
i  , to z pewnością
, to z pewnością 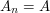 i
i 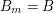 . Wtedy
. Wtedy 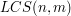 oznacza długość najdłuższego wspólnego podciągu dla całych wyrazów
oznacza długość najdłuższego wspólnego podciągu dla całych wyrazów 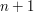 na
na 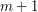 komórek, bowiem w komórce
komórek, bowiem w komórce 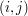 chcemy przechowywać liczbę
chcemy przechowywać liczbę 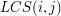 (dla
(dla 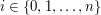 oraz
oraz 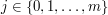 ). Druga obserwacja pozwoli nam na wpisanie do tej tablicy pewnej liczby początkowych wartości, wzór z obserwacji pierwszej posłuży do dalszego wypełniania komórek.
). Druga obserwacja pozwoli nam na wpisanie do tej tablicy pewnej liczby początkowych wartości, wzór z obserwacji pierwszej posłuży do dalszego wypełniania komórek.
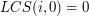 i
i 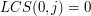 , to zerowy wiersz i zerową kolumnę tabeli wypełnić należy zerami.
, to zerowy wiersz i zerową kolumnę tabeli wypełnić należy zerami.


