Pochodne i krawędzie
20.04.2010 - Krzysztof Dryś
    Nadciąga druga pochodna
Naszym celem jest znalezienie miejsca, gdzie
Jak rozwiązać nasze równanie? W taki sam sposób, jak poprzednio - należy policzyć
To pozwoli zapisać nam następujący algorytm:
Jak znaleźć zera v[i,j]? Oczywiście najprościej zrobić to tak:
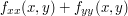 zwyczajnie nie wykryjemy. Dlaczego? Jeżeli v[i,j] = 1 oraz v[i+1,j] = -1, to wiemy że gdzie między punktem (i,j) a (i+1,j) jest zero. Ale nasz algorytm tego nie wykryje. Dlatego rzeczywiste algorytmy nie szukają tych pikseli, gdzie v[i,j] jest równe zero, tylko tych, gdzie v[i,j] zmienia znak. zwyczajnie nie wykryjemy. Dlaczego? Jeżeli v[i,j] = 1 oraz v[i+1,j] = -1, to wiemy że gdzie między punktem (i,j) a (i+1,j) jest zero. Ale nasz algorytm tego nie wykryje. Dlatego rzeczywiste algorytmy nie szukają tych pikseli, gdzie v[i,j] jest równe zero, tylko tych, gdzie v[i,j] zmienia znak.
 Wynik działania powyższego algorytmu. Na obrazku jest zdecydowanie za dużo krawędzi. I sporo szumów. Ale krawędzie tworzą zamknięte kształty. A większość z nich ma szerokość jednego piksela.
Wynik działania powyższego algorytmu. Na obrazku jest zdecydowanie za dużo krawędzi. I sporo szumów. Ale krawędzie tworzą zamknięte kształty. A większość z nich ma szerokość jednego piksela.
Spróbujmy ocenić powyższy obrazek. Wydaje się, że jest w nim za dużo krawędzi. Dlaczego tak jest? Spróbujmy jeszcze raz użyć nasz intuicji z jednego wymiaru. Szukamy miejsc, gdzie funkcja
Czy to nie zaskakujące, że sprawy takie jak: punkt przegięcia, maksimum i minimum, kojarzące się z czystą (i nudną!) teorią znajdują tutaj zastosowanie? Fajnie się przekonać, że wiedza z analizy matematycznej przydaje się w praktyce.
Po drugie, nawet jeżeli w Jak temu zaradzić? W artykule proste przetwarzanie obrazów można przeczytać o rozmywaniu obrazka. Zastosujemy ten trik, mając nadzieję, że po rozmyciu na obrazku zostaną na nim tylko ważne krawędzie. Daje nam to następujący algorytm:
Sposób rozmycia obrazka  Wynik działania algorytmu naszego przy zastosowaniu średniego rozmycia.
Wynik działania algorytmu naszego przy zastosowaniu średniego rozmycia.
 Wynik działania algorytmu naszego przy zastosowaniu mocnego rozmycia. Spowodowało ono, że krawędzie nie zostały zachowane i rozpłynęły się na wiele maksimów i minimów lokalnych. Na tym przykładzie widać, że wszystkich metod należy używać z umiarem i zastanowieniem. Trochę rozmycia daje dobre efekty, ale za dużo powoduje niespodziewane skutki.
Wynik działania algorytmu naszego przy zastosowaniu mocnego rozmycia. Spowodowało ono, że krawędzie nie zostały zachowane i rozpłynęły się na wiele maksimów i minimów lokalnych. Na tym przykładzie widać, że wszystkich metod należy używać z umiarem i zastanowieniem. Trochę rozmycia daje dobre efekty, ale za dużo powoduje niespodziewane skutki.
(1 ocena) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


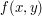 zmienia się najbardziej. Gdybyśmy operowali na funkcji jednej zmiennej
zmienia się najbardziej. Gdybyśmy operowali na funkcji jednej zmiennej 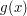 , oznaczałoby to rozwiązanie równania
, oznaczałoby to rozwiązanie równania 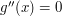 . My, żeby znaleźć krawędzie w dwóch wymiarach, będziemy rozwiązywać równanie:
. My, żeby znaleźć krawędzie w dwóch wymiarach, będziemy rozwiązywać równanie: 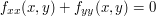 . Przez
. Przez 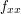 rozumiemy dwukrotne wzięcie pochodnej względem pierwszej zmiennej. Innymi słowy:
rozumiemy dwukrotne wzięcie pochodnej względem pierwszej zmiennej. Innymi słowy: 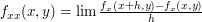 .
.
![$ u[i,j] $](/files/tex/2e9dc7e347097bd1458b207842a9c2bb19cc82fe.png) . Na przykład można
. Na przykład można ![$$u[i+2,j] + 2u[i+1,j] + 2u[i-1,j] + u[i-2,j] + $$](/files/tex/7d8358bfcee33c64f8cf3cddaac671d756e2a874.png)
![$$u[i,j+2] + 2u[i,j+1] + 2u[i,j-1] + u[i,j-2] - 16 u[i,j]$$](/files/tex/8d7e640bad024bf920738dac1e7d51ebdc68c980.png)
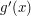 rozwiązując równanie
rozwiązując równanie  jest lokalne maksimum, to nie wiemy jeszcze, czy jest ono wystarczająco duże z globalnego punktu widzenia. Innymi słowy: nawet jeżeli w
jest lokalne maksimum, to nie wiemy jeszcze, czy jest ono wystarczająco duże z globalnego punktu widzenia. Innymi słowy: nawet jeżeli w  jest parametrem algorytmu. To znaczy: zależnie od tego, jakiej metody użyjmy i jak bardzo go rozmyjemy, dostaniemy różne wyniki.
jest parametrem algorytmu. To znaczy: zależnie od tego, jakiej metody użyjmy i jak bardzo go rozmyjemy, dostaniemy różne wyniki.


