Analiza matematyczna i analiza obrazów
Do tej pory nasz obraz był przechowywany w tablicy ![$ u[i,j] $](/files/tex/2e9dc7e347097bd1458b207842a9c2bb19cc82fe.png) . Załóżmy przez chwilę, że tak naprawdę obraz nasz jest funkcją
. Załóżmy przez chwilę, że tak naprawdę obraz nasz jest funkcją 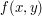 . Ta funkcja mówi jaka jest jasność poszczególnych punktów obrazu. Ale tym razem te punkty, to nie piksele. To punkty w sensie matematycznym. O ile pisząc
. Ta funkcja mówi jaka jest jasność poszczególnych punktów obrazu. Ale tym razem te punkty, to nie piksele. To punkty w sensie matematycznym. O ile pisząc ![$ u[i,j] $](/files/tex/2e9dc7e347097bd1458b207842a9c2bb19cc82fe.png) zakładamy, że znamy jasność skończonej ilości punktów, to pisząc
zakładamy, że znamy jasność skończonej ilości punktów, to pisząc 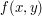 mamy na myśli rzeczywisty obraz, więc x oraz y mogą być dowolne.
mamy na myśli rzeczywisty obraz, więc x oraz y mogą być dowolne.
Jak szukalibyśmy krawędzi, gdybyśmy mieli dostęp do 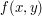 ? Krawędź to takie miejsce, gdzie
? Krawędź to takie miejsce, gdzie 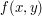 zmienia się najbardziej gwałtownie. Miarą zmienność funkcji, jest jej pochodna. Tak więc miejsce, gdzie pochodna
zmienia się najbardziej gwałtownie. Miarą zmienność funkcji, jest jej pochodna. Tak więc miejsce, gdzie pochodna 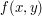 zmienia się najszybciej, to właśnie krawędzi. Aha, problemem może być to, że
zmienia się najszybciej, to właśnie krawędzi. Aha, problemem może być to, że 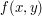 jest funkcją dwóch zmiennych. Jak policzyć jej pochodną?
jest funkcją dwóch zmiennych. Jak policzyć jej pochodną?
Najpierw przypomnijmy sobie, jak liczyć pochodne funkcji jednej zmiennej. Pochodną funkcji 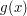 jest
jest 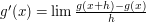 . Podobnie można zdefiniować pochodną funkcji
. Podobnie można zdefiniować pochodną funkcji 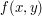 . Tylko, że funkcja dwóch zmiennych ma nie jedną a dwie pochodne! Jak to możliwe?
. Tylko, że funkcja dwóch zmiennych ma nie jedną a dwie pochodne! Jak to możliwe?
Pochodna 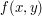 , względem pierwszego argumentu to:
, względem pierwszego argumentu to: 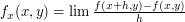 . Natomiast pochodna
. Natomiast pochodna 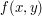 względem drugiego argumentu to:
względem drugiego argumentu to: 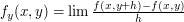 .
.
Pochodne funkcji wielu zmiennych to dosyć skomplikowana sprawa. Ale my nie chcemy ich zrozumieć. My chcemy je wykorzystać! Dlatego, na razie wystarczy nam wiedzieć, że liczy się je bardzo podobnie do zwykłych pochodnych. I mają bardzo podobne właściwości.
Jaki to wszystko ma związek z szukaniem krawędzi? My zamiast funkcji 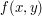 mamy do dyspozycji macierz
mamy do dyspozycji macierz ![$ u[i,j] $](/files/tex/2e9dc7e347097bd1458b207842a9c2bb19cc82fe.png) . Co prawda, nie można policzyć pochodnej z macierzy, ale można policzyć przybliżenie pochodnej. Co to znaczy? Popatrzmy na wzór:
. Co prawda, nie można policzyć pochodnej z macierzy, ale można policzyć przybliżenie pochodnej. Co to znaczy? Popatrzmy na wzór:
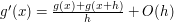
Mówi on, że pochodną można przybliżyć przez wyrażenie 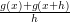 . Błąd przybliżenia wynosi
. Błąd przybliżenia wynosi 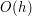 . Co to oznacza? Mówiąc najprościej: w najgorszym razie jest wprost proporcjonalny do
. Co to oznacza? Mówiąc najprościej: w najgorszym razie jest wprost proporcjonalny do 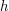 . Innymi słowy: jeżeli zmniejszymy
. Innymi słowy: jeżeli zmniejszymy 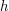 dwa razy, to błąd zmniejszy się również (przynajmniej) dwa razy!
dwa razy, to błąd zmniejszy się również (przynajmniej) dwa razy!
png.png)
Wykres funkcji
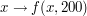
, czyli inaczej mówiąc przebieg jednego wiersza naszego obrazka. Gwałtowne zmiany funkcji odpowiadają krawędziom.
png.png)
Wykres funkcji
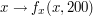
, czyli inaczej mówiąc przebieg przybliżenia pochodnej w jednym wierszu naszego obrazka. Miejsca, gdzie funkcja jest największa (bądź najmniejsza), odpowiadają
krawędziom.
I co z tego? Załóżmy, że w tablicy u[i,j] pamiętamy wartości funkcji 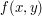 dla całkowitych par
dla całkowitych par 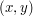 z pewnego przedziału. Wtedy, na podstawie tego co zobaczyliśmy przed chwilą, możemy wywnioskować, że
z pewnego przedziału. Wtedy, na podstawie tego co zobaczyliśmy przed chwilą, możemy wywnioskować, że ![$ u[i+1,j] - u[i,j] $](/files/tex/87ab343570c7dfa03bb7c7cb45dc3d953b40dc05.png) jest przybliżeniem
jest przybliżeniem 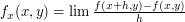 . Oznacza to, że na samym początku, nawet o tym nie wiedząc, liczyliśmy przybliżoną wartość pochodnej. Potem, wyznaczyliśmy punkty w których przybliżona pochodna ma największą wartość. I właśnie je oznaczyliśmy, jako zawierające krawędź.
. Oznacza to, że na samym początku, nawet o tym nie wiedząc, liczyliśmy przybliżoną wartość pochodnej. Potem, wyznaczyliśmy punkty w których przybliżona pochodna ma największą wartość. I właśnie je oznaczyliśmy, jako zawierające krawędź.
Wiemy już, jak działa nasz prosty filtr. Liczy on przybliżenie pochodnej, a następnie patrzy gdzie jest ono maksymalne. Czy teraz możemy go jakoś ulepszyć? Można zrobić to na dwa sposoby:
- Póki co,żeby znaleźć miejsca, gdzie
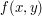 zmienia się najbardziej korzystaliśmy tylko
zmienia się najbardziej korzystaliśmy tylko 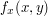 , czyli pochodnej względem pierwszego argumentu. Warto jednak wykorzystać również
, czyli pochodnej względem pierwszego argumentu. Warto jednak wykorzystać również 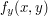 , czyli pochodną względem drugiego argumentu.
, czyli pochodną względem drugiego argumentu.
- Chcemy znaleźć miejsce, gdzie pochodna
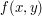 jest największa. Ale w tym celu również najlepiej użyć pochodnych! Warunkiem koniecznym na maksimum
jest największa. Ale w tym celu również najlepiej użyć pochodnych! Warunkiem koniecznym na maksimum 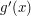 jest
jest 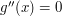 .
.




png.png) Wykres funkcji
Wykres funkcji 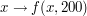 , czyli inaczej mówiąc przebieg jednego wiersza naszego obrazka. Gwałtowne zmiany funkcji odpowiadają krawędziom.
, czyli inaczej mówiąc przebieg jednego wiersza naszego obrazka. Gwałtowne zmiany funkcji odpowiadają krawędziom.
png.png) Wykres funkcji
Wykres funkcji 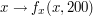 , czyli inaczej mówiąc przebieg przybliżenia pochodnej w jednym wierszu naszego obrazka. Miejsca, gdzie funkcja jest największa (bądź najmniejsza), odpowiadają
krawędziom.
, czyli inaczej mówiąc przebieg przybliżenia pochodnej w jednym wierszu naszego obrazka. Miejsca, gdzie funkcja jest największa (bądź najmniejsza), odpowiadają
krawędziom.


![$ u[i,j] $](/files/tex/2e9dc7e347097bd1458b207842a9c2bb19cc82fe.png) . Załóżmy przez chwilę, że tak naprawdę obraz nasz jest funkcją
. Załóżmy przez chwilę, że tak naprawdę obraz nasz jest funkcją 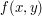 . Ta funkcja mówi jaka jest jasność poszczególnych punktów obrazu. Ale tym razem te punkty, to nie piksele. To punkty w sensie matematycznym. O ile pisząc
. Ta funkcja mówi jaka jest jasność poszczególnych punktów obrazu. Ale tym razem te punkty, to nie piksele. To punkty w sensie matematycznym. O ile pisząc 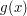 jest
jest 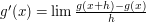 . Podobnie można zdefiniować pochodną funkcji
. Podobnie można zdefiniować pochodną funkcji 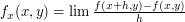 . Natomiast pochodna
. Natomiast pochodna 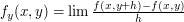 .
.
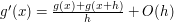
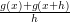 . Błąd przybliżenia wynosi
. Błąd przybliżenia wynosi 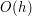 . Co to oznacza? Mówiąc najprościej: w najgorszym razie jest wprost proporcjonalny do
. Co to oznacza? Mówiąc najprościej: w najgorszym razie jest wprost proporcjonalny do 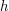 . Innymi słowy: jeżeli zmniejszymy
. Innymi słowy: jeżeli zmniejszymy 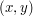 z pewnego przedziału. Wtedy, na podstawie tego co zobaczyliśmy przed chwilą, możemy wywnioskować, że
z pewnego przedziału. Wtedy, na podstawie tego co zobaczyliśmy przed chwilą, możemy wywnioskować, że ![$ u[i+1,j] - u[i,j] $](/files/tex/87ab343570c7dfa03bb7c7cb45dc3d953b40dc05.png) jest przybliżeniem
jest przybliżeniem 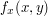 , czyli pochodnej względem pierwszego argumentu. Warto jednak wykorzystać również
, czyli pochodnej względem pierwszego argumentu. Warto jednak wykorzystać również 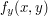 , czyli pochodną względem drugiego argumentu.
, czyli pochodną względem drugiego argumentu. 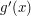 jest
jest 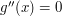 .
.

