Trwałe struktury danych
07.06.2010 - Filip Sieczkowski
    Kolejki: pierwsze starcieStandardowa ulotna implementacja kolejek (zarówno jedno- jak i dwustronnych) opiera się na łączonej liście dwukierunkowej. Jednak łatwość poruszania się po takiej liście, która powoduje że jest ona świetną strukturą ulotną, całkowicie uniemożliwia jej wykorzystanie w trwałym środowisku. Przypomnijmy sobie nasz poprzedni przykład drzew: podczas zmiany stanu struktury musieliśmy skopiować wszystkie wierzchołki, z których osiągalny był nowo dodany element. Ale w liście dwukierunkowej każdy element jest osiągalny z każdego innego, więc musielibyśmy za każdym razem kopiować całą strukturę. Takie rozwiązanie oczywiście nie wchodzi w rachubę. Okazuje się, że kolejki są jedną z najtrudniejszych do skutecznego zaimplementowania trwałych struktur danych (z klasycznych struktur trudniejsze są chyba tylko tablice); ich implementacji poświęcimy resztę artykułu.
Oczywiście, używając zbalansowanych drzew, możemy użyć kolejki priorytetowej zaimplementowanej z ich wykorzystaniem jako zwykłej kolejki FIFO. Jednak czas działania operacji Kolejka zamortyzowanaKluczowa dla konstrukcji naszej pierwszej kolejki jest obserwacja, że tak naprawdę w kolejce nie wykonuje się operacji znacząco różnych od stosu ─ po prostu jedną z operacji wykonujemy na innym końcu struktury, niż drugą. Pomysł jest tak naprawdę prosty: wystarczy trzymać początek kolejki w odwrotnej kolejności, niż koniec! W ten sposób i początek, i koniec kolejki może być listą, jak na poniższym rysunku.
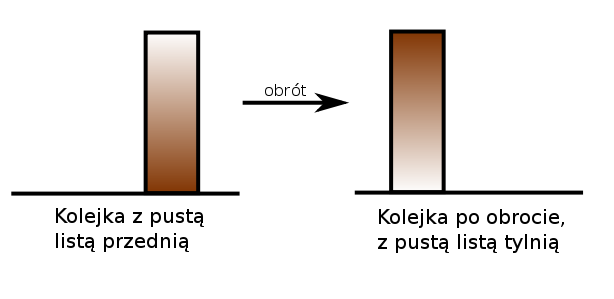
Pozostaje pytanie, co zrobić, kiedy lista ``przednia'', z której usuwamy, skończy się. Ale wtedy wystarczy tylko odwrócić ``ogon'' kolejki, jak na rysunku.
Oczywiście odwrócenie listy wymaga obejrzenia wszystkich jej elementów, więc zabiera
Porażka amortyzacji
Powyższa implementacja jest ładna i prosta, jednak niestety nie nadaje się do naszych zastosowań: nie można używać dawnych wersji kolejki. Wyobraźmy sobie, że zmienna
Taka sekwencja spowoduje, że tylną listę odwrócimy Istnieją metody, pozwalające na tworzenie trwałych struktur o koszcie zamortyzowanym, jednak są one wygodniejsze do stosowania w funkcyjnych językach programowania: w dalszej części artykułu skupimy się na innym, bardziej bezpośrednim, sposobie naprawienia naszych kolejek. Kolejki dwustronneKolejki dwustronne, zwane z angielska dequeue (od double-ended queue), są wariantem kolejek, w którym elementy można wstawiać i usuwać z każdej ze stron. Naturalną implementacją ulotnej kolejki jest oczywiście lista dwustronna, której podobnie jak przy zwykłej kolejce nie możemy użyć, jeśli chcemy mieć struktury trwałe. Zastosowanie przedstawionej wyżej zamortyzowanej kolejki bezpośrednio również nie jest możliwe ─ po obróceniu listy tylnej na przednią nie moglibyśmy usuwać elementów z końca kolejki. Okazuje się jednak, że trzeba zmienić bardzo niewiele: wystarczy zamiast przekładać całą listę ``wyrównać'' listę przednią i tylną. Żeby wyrównać długości list trzeba wiedzieć ile elementów trzeba przełożyć: najłatwiej to osiągnąć rozszerzając stan obliczeń o dodatkową liczbę, mówiącą o różnicy długości list. Wtedy, jeśli jedna z list się skończy, będziemy znali długość drugiej, a zatem będziemy mogli przenieść jej połowę na odpowiednią listę. Implementacja, również wykorzystująca poprzednio zdefiniowane struktury danych, wygląda następująco:
Oczywiście również tej kolejki nie możemy wykorzystać, jeśli chcemy używać starych stanów struktury. Jeśli jednak ich nie potrzebujemy, a z jakiegoś powodu używamy struktur trwałych, to powyższe kolejki są najszybszą i najprostszą implementacyjnie możliwością. Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


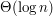 , który w ten sposób osiągniemy, nie jest satysfakcjonujący. Poniżej przedstawimy kolejkę działającą w zamortyzowanym czasie stałym i zobaczymy, czemu nie rozwiązuje ona naszych problemów. Zobaczymy też jak taką kolejkę przerobić na kolejkę dwustronną. W ostatniej części artykułu otrzymamy kolejkę, której wszystkie podstawowe operacje działają w czasie stałym, pozostawiając jako zadanie czytelnikowi zmierzenie się z kolejką dwustronną.
, który w ten sposób osiągniemy, nie jest satysfakcjonujący. Poniżej przedstawimy kolejkę działającą w zamortyzowanym czasie stałym i zobaczymy, czemu nie rozwiązuje ona naszych problemów. Zobaczymy też jak taką kolejkę przerobić na kolejkę dwustronną. W ostatniej części artykułu otrzymamy kolejkę, której wszystkie podstawowe operacje działają w czasie stałym, pozostawiając jako zadanie czytelnikowi zmierzenie się z kolejką dwustronną.

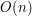 jednostek czasu. Jednak żeby trzeba było obrócić listę długości
jednostek czasu. Jednak żeby trzeba było obrócić listę długości  , musieliśmy
, musieliśmy 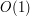 jednostek czasu), a więc mogliśmy na to odwrócenie listy ``zaoszczędzić'' w czasie wcześniejszych operacji. Poniżej przedstawiamy implementację takiej kolejki, z wykorzystaniem wcześniej zaprezentowanych list.
jednostek czasu), a więc mogliśmy na to odwrócenie listy ``zaoszczędzić'' w czasie wcześniejszych operacji. Poniżej przedstawiamy implementację takiej kolejki, z wykorzystaniem wcześniej zaprezentowanych list.
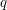 pokazuje na kolejkę, w której przedniej liście pozostał dokładnie jeden element, zaś tylna lista jest długa. Weźmy teraz sekwencję instrukcji:
pokazuje na kolejkę, w której przedniej liście pozostał dokładnie jeden element, zaś tylna lista jest długa. Weźmy teraz sekwencję instrukcji:
 razy a więc koszt zamortyzowany będzie rzędu
razy a więc koszt zamortyzowany będzie rzędu 

