Kolejki Hooda-Melville'a
Problem z przedstawioną wcześniej kolejką wynikał z dużej ilości pracy, którą trzeba było wykonać w jednym momencie, co drastycznie pogarszało złożoność. Pierwszy pomysł, jak poprawić implementację kolejek trwałych, pochodzący od Hooda i Melville'a, polega na następującej obserwacji:
Jeśli zaczniemy obracać listę tylną i doczepiać ją do przedniej odpowiednio wcześnie, i będziemy to robić powoli, po kilka kroków na każdą operację kolejki, to możemy otrzymać nową, gotową listę zanim stara się skończy.
Ogólny zarys działania przedstawia poniższy rysunek. Kiedy listy przednia i tylna osiągną równą długość, zaczynamy je odpowiednio łączyć. Łączenie to potrwa 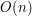 kroków, gdzie
kroków, gdzie  jest długością przedniej listy. Dzięki temu, jeśli pozostawimy przednią listę, i będziemy wykonywać stałą liczbę kroków obliczania nowej wersji w czasie każdej operacji kolejki, to nową wersję otrzymamy zanim stara lista zostanie wyczerpana.
jest długością przedniej listy. Dzięki temu, jeśli pozostawimy przednią listę, i będziemy wykonywać stałą liczbę kroków obliczania nowej wersji w czasie każdej operacji kolejki, to nową wersję otrzymamy zanim stara lista zostanie wyczerpana.
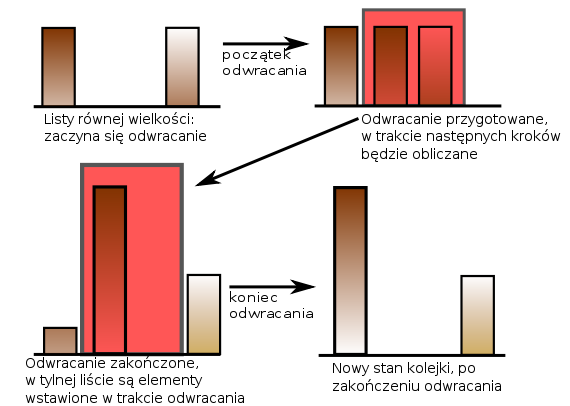
Jeśli zastanowimy się teraz, co się dzieje w czasie odwracania list w czerwonym prostokącie, zauważymy dwa problemy: po pierwsze, co zrobić z elementami wstawionymi i usuniętymi z kolejki w czasie odwracania, a po drugie, czy z tego powodu przednia lista nie stanie się krótsza niż tylna.
Pierwszy z tych problemów ma dwie części: elementy wstawione (jasnożółte na rysunku) nie stanowią problemu, gdyż na tylnej liście znajdują się tylko one i wystarczy jej po prostu nie zmieniać po wyliczeniu nowej przedniej listy. Z usunięciami z kolejki też można sobie łatwo poradzić, przestając odwracać kolejkę odpowiednio szybciej (kiedy pozostałe do odwrócenia elementy byłyby już usunięte).
Rozwiązanie drugiego problemu jest łatwiejsze: ponieważ obracanie ma trwać co najwyżej  instrukcji dla kolejki, więc w tym czasie suma ilości elementów usuniętych i wstawionych
instrukcji dla kolejki, więc w tym czasie suma ilości elementów usuniętych i wstawionych 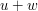 jest mniejsza od
jest mniejsza od  . Długość tylnej listy po wyliczeniu nowej wersji listy przedniej wynosi
. Długość tylnej listy po wyliczeniu nowej wersji listy przedniej wynosi 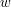 , zaś długość listy przedniej ─
, zaś długość listy przedniej ─ 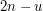 . Zatem, żeby lista tylna była dłuższa, musiałoby być
. Zatem, żeby lista tylna była dłuższa, musiałoby być 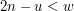 , czyli
, czyli 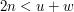 . Zatem, korzystając z ograniczenia na
. Zatem, korzystając z ograniczenia na 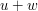 , dostajemy
, dostajemy 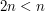 , co nie może być prawdą.
, co nie może być prawdą.
Pozostaje nam zatem już tylko jedno: jak, w czasie 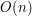 i wykonując
i wykonując 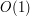 kroków dla każdej operacji na kolejce stworzyć nową listę. Łączenie będzie się odbywało w dwóch fazach: najpierw równocześnie będziemy odwracać obie listy (co zajmie
kroków dla każdej operacji na kolejce stworzyć nową listę. Łączenie będzie się odbywało w dwóch fazach: najpierw równocześnie będziemy odwracać obie listy (co zajmie  jednostek czasu), a kiedy ten etap się skończy, odwróconą listę przednią będziemy ``przekładać'' na odwróconą listę tylną. Takie przekładanie odwróci nam listę raz jeszcze, a więc dostaniemy listę przednią z dołączoną do niej z tyłu odwróconą listą tylną. Ta część zajmie co najwyżej
jednostek czasu), a kiedy ten etap się skończy, odwróconą listę przednią będziemy ``przekładać'' na odwróconą listę tylną. Takie przekładanie odwróci nam listę raz jeszcze, a więc dostaniemy listę przednią z dołączoną do niej z tyłu odwróconą listą tylną. Ta część zajmie co najwyżej  jednostek czasu (mniej jeśli z przedniej listy zostały usunięte jakieś elementy), a więc w sumie po
jednostek czasu (mniej jeśli z przedniej listy zostały usunięte jakieś elementy), a więc w sumie po 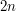 krokach nowy stan zostanie wyliczony. Zatem wystarczy wykonywać dwa kroki obliczania stanu na jedną operację kolejki. Gotowa implementacja przedstawiona jest poniżej.
krokach nowy stan zostanie wyliczony. Zatem wystarczy wykonywać dwa kroki obliczania stanu na jedną operację kolejki. Gotowa implementacja przedstawiona jest poniżej.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
| class RotationState {
public:
int state; // 0 - idle, 1 - done, 2 - rotating, 3 - appending
int diff;
List * fst, * snd, * thd, * fth;
RotationState(){
state = 0;
diff = 0;
fst = snd = thd = fth = List :: nil();
}
RotationState(List * f){
state = 1;
diff = 0;
fst = f;
snd = thd = fth = List :: nil();
}
RotationState(int d, List * f, List * s){
state = 3; diff = d; fst = f; snd = s; thd = fth = List :: nil();
}
RotationState(int d, List * f, List * s, List * t, List * k){
state = 2; diff = d; fst = f; snd = s; thd = t; fth = k;
}
RotationState * exec(){
if(state == 2) {
if(fst == List::nil()){
return new RotationState(diff, snd, List::cons(List::head(thd), fth));
}
return new RotationState(diff+1, List::tail(fst),
List::cons(List::head(fst), snd),
List::tail(thd), List::cons(List::head(thd), fth));
} else if (state == 3) {
if (diff == 0) return new RotationState(snd);
return new RotationState(diff-1, List::tail(fst),
List::cons(List::head(fst), snd));
} else return this;
}
RotationState * invalidate(){
if(state == 2){
return new RotationState(diff-1, fst, snd, thd, fth);
}else if(state == 3){
if (diff == 0) return new RotationState(List::tail(snd));
return new RotationState(diff-1, fst, snd);
}else return this;
}
};
class HMQueue {
private:
int lenf, lenr;
List * f, * r;
RotationState * state;
HMQueue(int lf, List * _f, RotationState * st, int lr, List * _r){
lenf = lf; lenr = lr;
f = _f; r = _r; state = st;
}
static HMQueue * check(int lf, List * f, RotationState * st, int lr, List * r){
RotationState * rs = st;
if(lr > lf){
RotationState * rs = new RotationState(0, f, List::nil(), r, List::nil());
lf += lr;
lr = 0;
r = List :: nil();
}
rs = rs->exec()->exec();
if(rs->state == 1){
return new HMQueue(lf, rs->fst, new RotationState(), lr, r);
}
return new HMQueue(lf, f, rs, lr, r);
}
public:
static HMQueue * snoc(int elem, HMQueue * q) {
return check(q->lenf, q->f, q->state, q->lenr+1, List::cons(elem, q->r));
}
int head() {
return List::head(f);
}
HMQueue * tail(){
return check(lenf-1, List::tail(f), state->invalidate(), lenr, r);
}
}; |
Klasa RotationState opisuje aktualny stan w czerwonym prostokącie, w którym
- może nic się nie dziać (stan idle)
- może znajdować się gotowa, obliczona nowa lista (stan done)
- mogą znajdować się dwie listy w trakcie odwracania na listy pomocnicze (stan rotating)
- mogą znajdować się dwie listy, z których jedna jest odwracana i doklejana do drugiej (stan appending)
Funkcja exec wykonuje pojedynczy krok wyliczania tego stanu, zaś funkcja invalidate, wywoływana przy operacji tail, powoduje, że doklejanie listy przedniej do tylnej skończy się o kolejny krok wcześniej.
Kolejka dwustronna
Podobnie jak w przypadku wcześniejszych kolejek dwustronnych, teraz też będzie trzeba długości list wyrównywać, jednak znów nie można czekać aż jedna z list zupełnie się skończy. Trik, który trzeba zastosować, polega na wybraniu małej stałej  (w praktyce 2 lub 3), i wyrównywaniu list kiedy jedna z list jest więcej niż
(w praktyce 2 lub 3), i wyrównywaniu list kiedy jedna z list jest więcej niż  razy krótsza od drugiej. Poza tym, w przypadku kolejki dwustronnej nie będzie już można po prostu zostawić dodanych elementów; trzeba je będzie odpowiednio dokleić do nowych wersji list.
razy krótsza od drugiej. Poza tym, w przypadku kolejki dwustronnej nie będzie już można po prostu zostawić dodanych elementów; trzeba je będzie odpowiednio dokleić do nowych wersji list.
Co dalej?
Oczywiście przedstawione tu przykłady w żadnym wypadku nie wyczerpują bogatego i wciąż dynamicznie się rozwijającego świata trwałych struktur danych. Zainteresowany czytelnik powinien rozpocząć dalszą drogę od znakomitej, choć niestety trudno dostępnej i dotychczes nieprzetłumaczonej na polski, książki Chrisa Okasakiego "Purely Functional Data Structures." Wymaga ona pewnej znajomości programowania funkcjonalnego, co jednak w przypadku zajmowania się trwałymi strukturami jest chyba niemożliwe do uniknięcia.
Zapraszam też do rozwiązywania dołączonych do artykułu zadań. Bawcie się dobrze!
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany.
Zaloguj się lub
załóż konto.






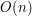 kroków, gdzie
kroków, gdzie  jest długością przedniej listy. Dzięki temu, jeśli pozostawimy przednią listę, i będziemy wykonywać stałą liczbę kroków obliczania nowej wersji w czasie każdej operacji kolejki, to nową wersję otrzymamy zanim stara lista zostanie wyczerpana.
jest długością przedniej listy. Dzięki temu, jeśli pozostawimy przednią listę, i będziemy wykonywać stałą liczbę kroków obliczania nowej wersji w czasie każdej operacji kolejki, to nową wersję otrzymamy zanim stara lista zostanie wyczerpana.

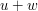 jest mniejsza od
jest mniejsza od 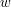 , zaś długość listy przedniej ─
, zaś długość listy przedniej ─ 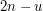 . Zatem, żeby lista tylna była dłuższa, musiałoby być
. Zatem, żeby lista tylna była dłuższa, musiałoby być 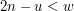 , czyli
, czyli 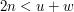 . Zatem, korzystając z ograniczenia na
. Zatem, korzystając z ograniczenia na 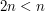 , co nie może być prawdą.
, co nie może być prawdą.
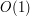 kroków dla każdej operacji na kolejce stworzyć nową listę. Łączenie będzie się odbywało w dwóch fazach: najpierw równocześnie będziemy odwracać obie listy (co zajmie
kroków dla każdej operacji na kolejce stworzyć nową listę. Łączenie będzie się odbywało w dwóch fazach: najpierw równocześnie będziemy odwracać obie listy (co zajmie 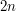 krokach nowy stan zostanie wyliczony. Zatem wystarczy wykonywać dwa kroki obliczania stanu na jedną operację kolejki. Gotowa implementacja przedstawiona jest poniżej.
krokach nowy stan zostanie wyliczony. Zatem wystarczy wykonywać dwa kroki obliczania stanu na jedną operację kolejki. Gotowa implementacja przedstawiona jest poniżej.
 (w praktyce 2 lub 3), i wyrównywaniu list kiedy jedna z list jest więcej niż
(w praktyce 2 lub 3), i wyrównywaniu list kiedy jedna z list jest więcej niż 

