Trwałe struktury danych
07.06.2010 - Filip Sieczkowski
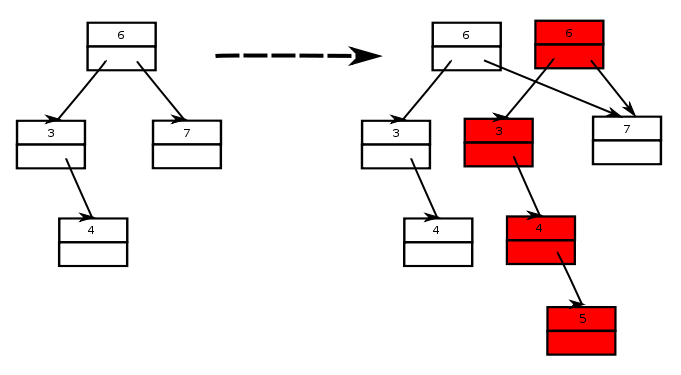
    Coś więcej: drzewa przeszukiwań binarnychJak widzieliśmy, stos w wersji trwałej w zasadzie nie różnił się od zwykłego stosu, do jakiego byliśmy przyzwyczajeni. Dzieje się tak, ponieważ nowo dodawany element nie będzie osiągalny z żadnego spośród elementów stosu. W przypadku drzewa BST, nowe elementy dodajemy w liściach drzewa, a więc muszą być one osiągalne z jego korzenia. Jednocześnie samego korzenia nie możemy zmodyfikować ─ z niego ``widoczna'' ma być stara wersja drzewa. Sposobem na poradzenie sobie z tym problemem jest technika kopiowania ścieżki ─ Skopiowane zostaną wszystkie elementy drzewa, z których widoczny jest nowo dodawany element, a więc ścieżka od korzenia aż do miejsca, w które nasz element zostanie wstawiony. Zobaczmy to na przykładzie wstawienia do drzewa elementu o kluczu 5. Elementy pokolorowane na czerwono zostały stworzone w trakcie operacji insert. Jak widać, został stworzony element o kluczu 5, a ścieżka prowadząca do niego od korzenia została skopiowana. Części drzewa poza ścieżką są współdzielone.
Poniżej przedstawiona jest implementacja drzewa BST z operacjami wstawiania, znajdowania i usuwania minimum, oraz znajdowania dolnego ograniczenia dla danego klucza.
Zwróćmy uwagę, jak w funkcjach zmieniających drzewo (delete_min i insert), cała ścieżka od drzewa do odpowiedniego węzła jest kopiowana, podczas gdy odpowiednie poddrzewa pozostają niezmienionymi wskaźnikami ─ a więc są współdzielone z poprzednią wersją struktury. Dokładnie taki był nasz cel, opisany na rysunku. Oczywiście taką implementację drzew BST można, podobnie jak wersję ulotną, usprawnić tworząc trwałe drzewa AVL lub czerwono-czarne; odpowiednia modyfikacja (bez usuwania elementów) jest przedmiotem drugiego z zadań. Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com