Indywidualiści – grafy mające swoje oznaczenia:
Grafem pełnym
nazywamy graf, w którym każda para wierzchołków jest połączona i
oznaczamy go 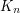 gdzie
gdzie  to liczba wierzchołków. Rozgrywki w systemie
‘każdy z każdym’ można opisać za pomocą grafu pełnego.
to liczba wierzchołków. Rozgrywki w systemie
‘każdy z każdym’ można opisać za pomocą grafu pełnego.
Zad.2 Ile krawędzi jest w grafie 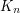 ?
?
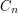 oznacza graf cykliczny o
oznacza graf cykliczny o  wierzchołkach. Jest to graf spójny (tzn.
taki, w którym z każdego wierzchołka da się przejść do innego), którego
każdy wierzchołek jest stopnia
wierzchołkach. Jest to graf spójny (tzn.
taki, w którym z każdego wierzchołka da się przejść do innego), którego
każdy wierzchołek jest stopnia 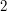 .
.
Jeśli zbiór wierzchołków grafu
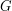 możemy podzielić na dwa rozłączne zbiory
możemy podzielić na dwa rozłączne zbiory  i
i  w taki sposób, że
każda krawędź łączy wierzchołek ze zbioru
w taki sposób, że
każda krawędź łączy wierzchołek ze zbioru  z wierzchołkiem ze zbioru
z wierzchołkiem ze zbioru
 to graf taki nazywamy dwudzielnym. Dla zilustrowania takiego grafu, możemy pomyśleć sobie o sforze i lisach. Każdy pies poluje na jakiegoś lisa, ale ani psy, ani lisy nie polują na członków swojego stada.
to graf taki nazywamy dwudzielnym. Dla zilustrowania takiego grafu, możemy pomyśleć sobie o sforze i lisach. Każdy pies poluje na jakiegoś lisa, ale ani psy, ani lisy nie polują na członków swojego stada.
Spróbujmy teraz znaleźć rozwiązanie pewnej gry:
Mamy
do dyspozycji  kostki, których ścianki są pokolorowane jednym z
czeterech kolorów: żółtym, czerwonym, niebieskim i zielonym. Czy można
ułożyć wieżę ze wszystkich czterech klocków tak, aby na każdej ścianie
wieży wystąpił każdy kolor?
kostki, których ścianki są pokolorowane jednym z
czeterech kolorów: żółtym, czerwonym, niebieskim i zielonym. Czy można
ułożyć wieżę ze wszystkich czterech klocków tak, aby na każdej ścianie
wieży wystąpił każdy kolor?
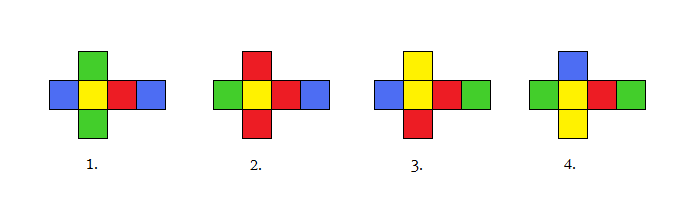
Skoro cały czas mówimy o grafach, to musimy ich użyć, żeby to rozwiązać :)
Narysujmy
grafy tych kostek: wierzchołkami będą kolory, a krawędzie będą łączyły
te z nich, które występują na przeciwległych ścianach.
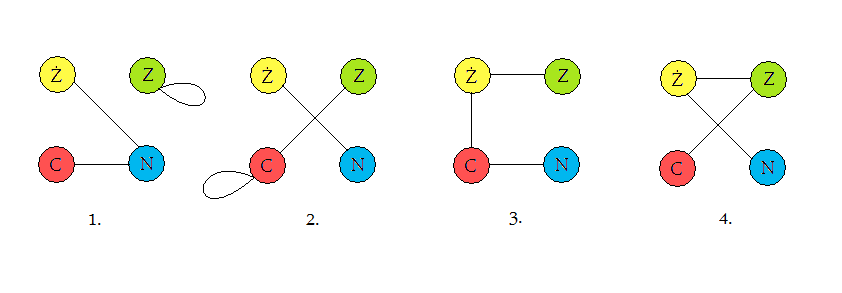
‘Sklejmy’ teraz te wszystkie grafy w jeden multigraf:
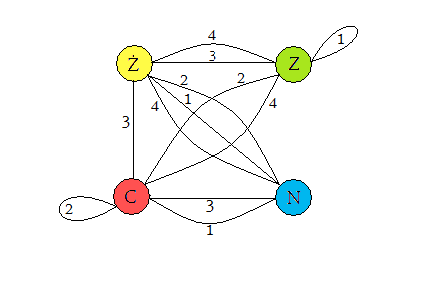
Teraz
rozwiązaniem będzie znalezienie dwóch takich podgrafów 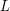 ,
,  , które będą
miały te same zbiory wierzchołków co nasz multigraf (wszystkie kolory),
każda krawędź w podgrafie będzie o innym numerze (jeśli ustalimy już
pozycję dla
, które będą
miały te same zbiory wierzchołków co nasz multigraf (wszystkie kolory),
każda krawędź w podgrafie będzie o innym numerze (jeśli ustalimy już
pozycję dla  . kostki, to nie możemy jej zmieniać), żadne krawędzie nie
będą wspólne oraz oba podgrafy będą miały wierzchołki tylko
. kostki, to nie możemy jej zmieniać), żadne krawędzie nie
będą wspólne oraz oba podgrafy będą miały wierzchołki tylko 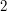 stopnia
(to zagwarantuje, że każdy kolor pojawi się dokładnie po jednym razie
na ściankach).
stopnia
(to zagwarantuje, że każdy kolor pojawi się dokładnie po jednym razie
na ściankach). 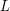 będzie reprezentował ustawienie kolorów na ścianie
lewej i prawej, a
będzie reprezentował ustawienie kolorów na ścianie
lewej i prawej, a  ustawienie na ścianie przedniej i tylnej.
ustawienie na ścianie przedniej i tylnej.
Zanim
przejdziemy dalej, przeczytajmy ten fragment jeszcze raz – to ważne
żebyśmy wiedzieli jakich własności wymagamy od szukanych grafów, a co
za tym idzie znaleźli poprawne ustawienie. Zapiszmy sobie rozwiązanie
na kartce (żeby się czegoś nauczyć, sami musimy tego spróbować :)).
Skoro mamy już rozrysowaną wierzę, to porównajmy ją z poniższym
rysunkiem:
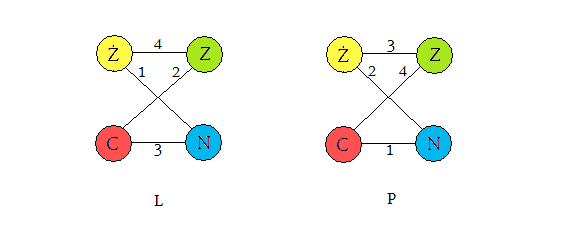
Mamy za sobą spory wstęp do teorii grafów, teraz nie pozostaje nam nic innego jak wykorzystać tę wiedzę w praktyce. Zapraszam zatem do rozwiązania prostych zadań, które pomogą nabrać intuicji do odnajdywania w problemie ukrytych grafów :)



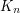 gdzie
gdzie  to liczba wierzchołków. Rozgrywki w systemie
‘każdy z każdym’ można opisać za pomocą grafu pełnego.
to liczba wierzchołków. Rozgrywki w systemie
‘każdy z każdym’ można opisać za pomocą grafu pełnego.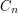 oznacza graf cykliczny o
oznacza graf cykliczny o 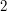 .
.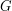 możemy podzielić na dwa rozłączne zbiory
możemy podzielić na dwa rozłączne zbiory  i
i  w taki sposób, że
każda krawędź łączy wierzchołek ze zbioru
w taki sposób, że
każda krawędź łączy wierzchołek ze zbioru  kostki, których ścianki są pokolorowane jednym z
czeterech kolorów: żółtym, czerwonym, niebieskim i zielonym. Czy można
ułożyć wieżę ze wszystkich czterech klocków tak, aby na każdej ścianie
wieży wystąpił każdy kolor?
kostki, których ścianki są pokolorowane jednym z
czeterech kolorów: żółtym, czerwonym, niebieskim i zielonym. Czy można
ułożyć wieżę ze wszystkich czterech klocków tak, aby na każdej ścianie
wieży wystąpił każdy kolor?


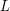 ,
,  , które będą
miały te same zbiory wierzchołków co nasz multigraf (wszystkie kolory),
każda krawędź w podgrafie będzie o innym numerze (jeśli ustalimy już
pozycję dla
, które będą
miały te same zbiory wierzchołków co nasz multigraf (wszystkie kolory),
każda krawędź w podgrafie będzie o innym numerze (jeśli ustalimy już
pozycję dla  . kostki, to nie możemy jej zmieniać), żadne krawędzie nie
będą wspólne oraz oba podgrafy będą miały wierzchołki tylko
. kostki, to nie możemy jej zmieniać), żadne krawędzie nie
będą wspólne oraz oba podgrafy będą miały wierzchołki tylko 


