Rodzaje grafów
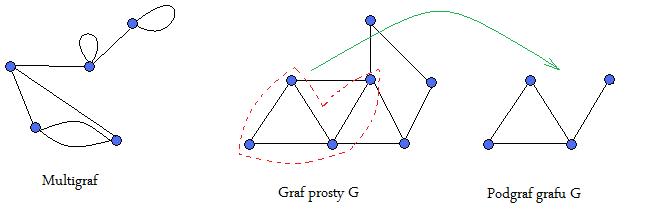
Multigrafem (często mówiąc ‘graf’ mamy na myśli właśnie ten rodzaj grafów) nazywamy graf, w którym występują pętle i krawędzie wielokrotne. Multigrafy możemy dostrzec patrząc na jakąś mapę samochodową: zazwyczaj jest więcej niż jedna droga pomiędzy dwoma miastami, a i nikt nie zabroni nam wyjechać kawałek za miasto, a potem do niego zawrócić (nie odwiedzając przy tym innego miasta).
Z kolei gdybyśmy chcieli przedstawić na rysunku, którzy z pośród członków naszych rodzin są rodzeństwem, to narysowalibyśmy graf prosty. Ja nie mógłbym być swoim rodzeństwem, ani też nie mógłbym być rodzeństwem swojej siostry więcej niż jeden raz :). Zatem w grafie prostym NIE ma pętli ani krawędzi wielokrotnych.
Zad1. Czy potrafisz powiedzieć ile jest grafów prostych o n wierzchołkach?
Tu można zobaczyć odpowiedź
W grafie prostym nie ma pętli ani krawędzi wielokrotnych, zatem z każdego z  wierzchołków możemy poprowadzić krawędź do każdego z
wierzchołków możemy poprowadzić krawędź do każdego z 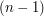 wierzchołków. Pamiętajmy jednak, że jeśli połączymy krawędzią wierzchołek
wierzchołków. Pamiętajmy jednak, że jeśli połączymy krawędzią wierzchołek  z
z  , to nie możemy połączyć już
, to nie możemy połączyć już  z
z  . Mamy zatem
. Mamy zatem 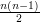 krawędzi. Narysujmy na kartce
krawędzi. Narysujmy na kartce  wierzchołków i weźmy wszystkie krawędzie w garść. Teraz dla każdej krawędzi decydujemy czy ją rysujemy, czy wyrzucamy. Mamy zatem
wierzchołków i weźmy wszystkie krawędzie w garść. Teraz dla każdej krawędzi decydujemy czy ją rysujemy, czy wyrzucamy. Mamy zatem 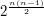 możliwości narysowania krawędzi co jest równe liczbie grafów prostych na n wierzchołkach.
możliwości narysowania krawędzi co jest równe liczbie grafów prostych na n wierzchołkach.
Podgrafem grafu G, nazywamy taki graf H, którego wszystkie wierzchołki należą do V(G), a krawędzie do E(G). Wracając do zagadki z meczami: gdybyśmy narysowali graf rozgrywek, to przykładem podgrafu, mógłby być kawałek pokazujący wszystkie mecze drużyny A oraz mecze, które rozegrały jej przeciwnicy (tj. wierzchołkami byłyby te drużyny, z którymi A zagrała, a krawędziami wszystkie mecze jakie odbyły się między nimi).
Czy z Wrocławia do Poznania prowadzi ścieżka, czy droga?
No właśnie, do tej pory używaliśmy słowo ‘droga’ mając na myśli drogę samochodową, ale patrząc na mapę jak na graf moglibyśmy powiedzieć, że z Wrocławia do Poznania istnieje zarówno ścieżka, jak i droga.
Ścieżką w grafie nazywamy skończony ciąg krawędzi 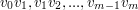 , w której wszystkie krawędzie są różne (gdyby nie były różne, to mielibyśmy do czynienia z trasą). Często stosuje się zapis postaci:
, w której wszystkie krawędzie są różne (gdyby nie były różne, to mielibyśmy do czynienia z trasą). Często stosuje się zapis postaci: 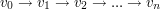 .
.
Ścieżkę możemy kojarzyć ze szlakiem turystycznym – możemy zatrzymywać się kilka razy w jednym schronisku, ale nie chcemy chodzić po tych samych szlakach.
Jeżeli dodatkowo nałożymy ograniczenie, że wszystkie wierzchołki w ścieżce są różne, to taka ścieżka będzie nazywana drogą. Jeżeli każda para wierzchołków, jest połączona drogą, to graf jest spójny ( to jest: jeśli z każdego wierzchołka da się przejść do każdego innego).
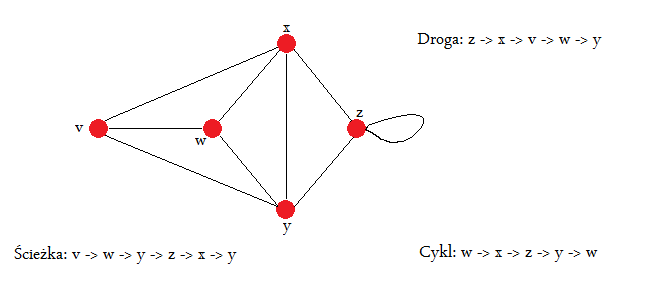
Drogę (tę w grafie) możemy kojarzyć z drogą (jezdnią) z miasta  do miasta
do miasta  : jeśli w trakcie jazdy odwiedzimy jakieś miasto
: jeśli w trakcie jazdy odwiedzimy jakieś miasto  więcej niż jeden raz, to znaczy że źle skręciliśmy na którejś obwodnicy i nadłożyliśmy kilometrów, podobnie jeżeli przez jakiś fragment drogi jechaliśmy więcej niż raz, tzn. że zabłądziliśmy i niepotrzebnie pokonaliśmy kilka kilometrów.
więcej niż jeden raz, to znaczy że źle skręciliśmy na którejś obwodnicy i nadłożyliśmy kilometrów, podobnie jeżeli przez jakiś fragment drogi jechaliśmy więcej niż raz, tzn. że zabłądziliśmy i niepotrzebnie pokonaliśmy kilka kilometrów.
Jeżeli pierwszy wierzchołek ścieżki jest równy ostatniemu, to taką ścieżkę nazywamy cyklem.
Przerwa na łamigłówkę: Czy potrafisz narysować poniższy rysunek nie odrywając ołówka od kartki i nie rysując po już narysowanych krawędziach?
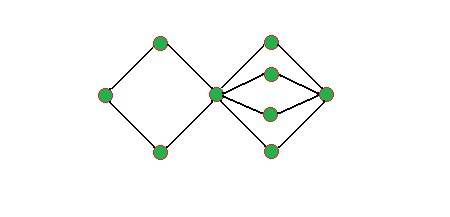
Owszem, zagadka jest ‘ze szkolnej ławy’, ale tak na prawdę taką łamigłówkę trzeba rozwiązać w większości film transportowych czy komunikacji miejskiej! Wyobraźmy sobie sytuację, w której jesteśmy w zarządzie komunikacji miejskiej i zamiast kreślić taki rysunek ołówkiem, jeździmy po mapie autobusem (lubimy się bawić samochodzikami:)). Chcielibyśmy aby autobus spalił jak najmniej paliwa i jednocześnie przejechał jak najwięcej tras (najlepiej wszystkie!). Jeżeli będzie jeździł kilka razy tym samym odcinkiem, to z pewnością nie zaoszczędzimy na paliwie. Zatem najfajniejsza byłaby trasa, która przebiega przez wszystkie ulice i w dodatku przez każdą dokładnie raz – czyli szukamy tu odpowiedzi na to samo pytanie co w naszej łamigłówce.
Obie sytuacje możemy opisać grafami, zatem sformułujmy to pytanie w języku grafów:
Czy w danym grafie istnieje cykl przechodzący przez każdą krawędź dokładnie jeden raz?
Okazuje się, że jest to ważny problem, czego może dowodzić fakt, że ktoś się juz nim zajął i go rozwiązał. Taki cykl nazywamy cyklem Eulera, bo tak się nazywał matematyk, który rozwiązał ten problem – wspomniany we wstępie artykułu. Dzięki niemu możemy zapisać następujące twierdzenie:
W grafie spójnym 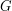 istnieje cykl Eulera wtedy i tylko wtedy, gdy stopień każdego wierzchołka grafu
istnieje cykl Eulera wtedy i tylko wtedy, gdy stopień każdego wierzchołka grafu 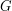 jest liczbą parzystą.
jest liczbą parzystą.
Graf w którym istnieje cykl Eulera nazywam grafem eulerowskim, a graf w którym istnieje ścieżka zawierająca każdą krawędź (ale kończąca się w innym od początkowego punkcie) jest grafem półeulerowskim.



 wierzchołków możemy poprowadzić krawędź do każdego z
wierzchołków możemy poprowadzić krawędź do każdego z 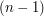 wierzchołków. Pamiętajmy jednak, że jeśli połączymy krawędzią wierzchołek
wierzchołków. Pamiętajmy jednak, że jeśli połączymy krawędzią wierzchołek  z
z  , to nie możemy połączyć już
, to nie możemy połączyć już 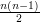 krawędzi. Narysujmy na kartce
krawędzi. Narysujmy na kartce 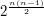 możliwości narysowania krawędzi co jest równe liczbie grafów prostych na n wierzchołkach.
możliwości narysowania krawędzi co jest równe liczbie grafów prostych na n wierzchołkach.
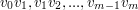 , w której wszystkie krawędzie są różne (gdyby nie były różne, to mielibyśmy do czynienia z trasą). Często stosuje się zapis postaci:
, w której wszystkie krawędzie są różne (gdyby nie były różne, to mielibyśmy do czynienia z trasą). Często stosuje się zapis postaci: 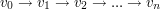 .
. 
 więcej niż jeden raz, to znaczy że źle skręciliśmy na którejś obwodnicy i nadłożyliśmy kilometrów, podobnie jeżeli przez jakiś fragment drogi jechaliśmy więcej niż raz, tzn. że zabłądziliśmy i niepotrzebnie pokonaliśmy kilka kilometrów.
więcej niż jeden raz, to znaczy że źle skręciliśmy na którejś obwodnicy i nadłożyliśmy kilometrów, podobnie jeżeli przez jakiś fragment drogi jechaliśmy więcej niż raz, tzn. że zabłądziliśmy i niepotrzebnie pokonaliśmy kilka kilometrów.
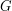 istnieje cykl Eulera wtedy i tylko wtedy, gdy stopień każdego wierzchołka grafu
istnieje cykl Eulera wtedy i tylko wtedy, gdy stopień każdego wierzchołka grafu 

