Wstęp do Teorii Grafów
10.12.2009 - Kacper Król
 Zadania
PługLimit czasowy: 1s; Limit pamięciowy: 16MB; Zbliża się zima i Stefana czekają ciężkie dni, bowiem jest kierowcą śnieżnego pługu. Robota lekką nie jest, a że Stefan nie jest w ciemię bity, to chciałby wcześniej zaplanować sobie pracę, tak by mieć więcej wolnego czasu. Wiadomo, że odśnieżyć trzeba każdą drogę, ale Stefan chciałby wiedzieć, czy może to zrobić w taki sposób, by nie jeździć po już odśnieżonych drogach. Znając plan połączeń pomiędzy skrzyżowaniami w mieście, pomóż Stefanowi by tym razem zima nie zaskoczyła drogowców. Wiemy, że Stefan pragnie wrócić na skrzyżowanie, z którego rozpoczął podróż. Wejście: Na wejściu podany jest opis dzielnicy, którą tym razem ma odśnieżyć Stefan. Opis składa się z par liczb
Przykład: Wejście: 1 2 Wyjście: TAK
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
ZenonLimit czasowy: 1s; Limit pamięciowy: 16MB; Zenon dołączył w grudniu do nowej klasy. Jak to zwykle bywa w takich sytuacjach, czuje się trochę nieswojo, gdyż nie zdążył jeszcze nikogo poznać. Integracje z klasą utrudnia mu fakt, że jest bardzo nieśmiały, ale za to jest dość błyskotliwy. Pomyślał, że jeśli pozna w klasie najpopularniejszą osobę, to dzięki takim kontaktom szybciej zintegruje się w nowej klasie, niż gdyby miał się zapoznać z każdym z uczniów. O popularności osoby
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. (6 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 ,
, 
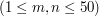 , które oznaczają, że ze skrzyżowania o numerze
, które oznaczają, że ze skrzyżowania o numerze  świadczy fakt, ile osób uważa ją za popularną. Jeżeli osoba
świadczy fakt, ile osób uważa ją za popularną. Jeżeli osoba  uważa osobę
uważa osobę 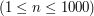 . Dla ułatwienia, zamiast imion i nazwisk uczniów, będziemy używać ich numerów z dziennika. Osób w klasie będzie nie więcej niż
. Dla ułatwienia, zamiast imion i nazwisk uczniów, będziemy używać ich numerów z dziennika. Osób w klasie będzie nie więcej niż 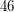 .
.

