Krótki wstęp do algorytmów geometrycznych
09.12.2009 - Dominik Rusak
 Geometria jest dziedziną matematyki, która zazwyczaj budzi rozmaite, najcześciej przeciwstawne uczucia. Jedni uważają ja za nudną - tym się dziwię. Inni dostrzegają piękno zajmowania się obiektami geometrycznymi, wymagającego pomysłowości, cierpliwości i nieraz chwili iluminacji. Wiele zadań geometrycznych da się rozwiązać w sposób żmudny i siłowy, lecz chwila olśnienia lub obycie w temacie pozwala odkryć "królewską drogę", prowadzącą szybko i błyskotliwie do rozwiązania. Geometria ma swoje miejsce też i w informatyce. Problemy geometryczne pojawiają się w grafice komputerowej, robotyce, statystyce i wielu innych dziedzinach. Przydatną jest zatem umiejetność stosowania algorytmów, pozwalających zautomatyzować działania wykonywane na obiektach geometrycznych. Dział informatyki zajmujący się takimi algorytmami zwie się geometria obliczeniową. Nadmienić należy, że zautomatyzowania takich działań nie należy zaliczać do wspomnianych "rozwiązań żmudnych i siłowych". Jest nie lada sztuką w sposób optymalny przetwarzać obiekty geometryczne. Wymaga to znajdowania i uogólniania "dróg królewskich", co wiąże się często z potrzebą dowiedzenia poprawności dla przypadku ogólnego. Częstokroć problemy geometryczne naszpikowane są "przypadkami brzegowymi", które należy z zegarmistrzowską precyzją wyławiać i rozpatrywać osobno.
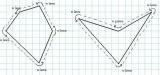
Będziemy badać rozmaite interakcje między odcinkami. Najpierw zastanowimy się, jak w łatwy sposób odpowiadać na pytanie, czy dla dwóch odcinków skierowanych o wspólnym początku pierwszy z nich jest położony zgodnie czy przeciwnie do ruchu wskazówek zegara względem drugiego. Informacja o takim wzajemnym położeniu dwóch odcinków jest bardzo ważna, gdyż pozwoli nam później powiedzieć coś o "chodzeniu po odcinkach", lub stwierdzić, czy pewne odcinki przecinają się. Zagadnienie to związane jest z polem takiego równoległoboku:
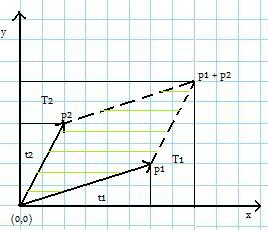
Spróbujmy obliczyć to pole, mając dane współrzędne punktów
Pole prostokąta to
(13 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


 i
i 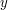 i zapisywać jako
i zapisywać jako 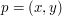 . Sumą dwóch punktów
. Sumą dwóch punktów 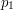 i
i 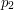 jest punkt
jest punkt 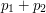 o współrzędnych
o współrzędnych 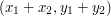 . Odcinek będzie przedstawiony jako para punktów, będących jego końcami. Mówiąc, że punkt
. Odcinek będzie przedstawiony jako para punktów, będących jego końcami. Mówiąc, że punkt 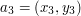 leży na prostej pomiędzy punktami
leży na prostej pomiędzy punktami 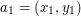 i
i 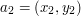 (wszystkie trzy są współliniowe), nie będziemy zakładać, że
(wszystkie trzy są współliniowe), nie będziemy zakładać, że 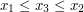 , lecz, że
, lecz, że 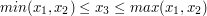 . Innymi słowy nie zakładamy wtedy, że to
. Innymi słowy nie zakładamy wtedy, że to 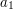 jest początkiem odcinka, patrząc od lewej strony. Odcinek skierowany będzie to uporządkowana para punktów. Wektorem nazwiemy odcinek uporządkowany, którego pierwszy punkt jest środkiem układu współrzędnych. Zanim przejdziemy do właściwej części artykułu, musimy odpowiedzieć na pytanie: czym właściwie jest odcinek na płaszczyźnie?
jest początkiem odcinka, patrząc od lewej strony. Odcinek skierowany będzie to uporządkowana para punktów. Wektorem nazwiemy odcinek uporządkowany, którego pierwszy punkt jest środkiem układu współrzędnych. Zanim przejdziemy do właściwej części artykułu, musimy odpowiedzieć na pytanie: czym właściwie jest odcinek na płaszczyźnie?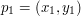 i
i 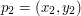 . Jest to dowolny punkt
. Jest to dowolny punkt 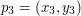 ,taki, że dla pewnej liczby
,taki, że dla pewnej liczby  z przedziału
z przedziału 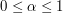 zachodzi:
zachodzi: 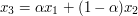 ,
, 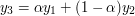 . Wygląda to dziwnie, lecz odcinek
. Wygląda to dziwnie, lecz odcinek 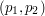 jest właśnie zbiorem kombinacji wypukłych
jest właśnie zbiorem kombinacji wypukłych 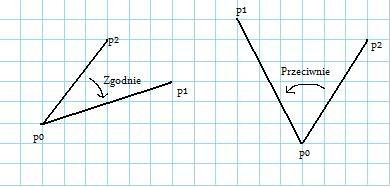
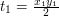 ,
, 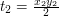 ,
, 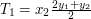 ,
,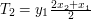 .
.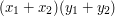 , zatem po elementarnych obliczeniach okazuje się, że pole równoległoboku wynosi
, zatem po elementarnych obliczeniach okazuje się, że pole równoległoboku wynosi 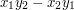 . Zauważmy, że wynika z tego, iż może ono być ujemne. Okazuje się, że taką samą wartość przyjmuje iloczyn wektorowy wektorów
. Zauważmy, że wynika z tego, iż może ono być ujemne. Okazuje się, że taką samą wartość przyjmuje iloczyn wektorowy wektorów 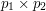 . Gdy jest on ujemny, punkt
. Gdy jest on ujemny, punkt 

