Przejdźmy do czegoś jeszcze ciekawszego. Chcemy odpowiadać na pytanie, czy dwa dane odcinki się przecinają. Można to zrobić bezpośrednio - wyznaczyć równania prostych, przechodzących przez te odcinki, znaleźć punkt ich przecięcia i zobaczyć, czy należy on do obu odcinków. Jednak będziemy musieli wtedy dzielić przy próbie znalezienia punktu przecięcia tych prostych. Problemy mogą się pojawić też, gdy jeden lub oba odcinki są równoległe do osi Y. Dzielenie jest kosztowną operacją, pojawiają się też często przy jego wykonywaniu błędy zaokrągleń, związane z reprezentacją liczb w komputerze. Jeżeli odcinki są prawie równoległe, komputer może stwierdzić, że tak obliczone proste je zawierające są dosłownie równoległe, i nie znaleźć ewentualnego punktu przecięcia.
Wolelibyśmy zatem ograniczyć się do dokładniejszych operacji, takich jak dodawanie, odejmowanie, mnożenie i porównywanie. Zastanówmy się zatem, co w obliczu omówionych już zagadnień oznacza przecinanie się odcinków? Zakładamy, że odcinki przecinają się, gdy mają co najmniej jeden punkt wspólny (mogą mieć nieskończenie dużo takich punktów wspólnych).
Zauważmy, że odcinki 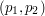 i
i 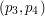 przecinają się, gdy każdy z nich przecina prostą, zawierającą drugi. Odcinek przecina prostą, gdy jego końce są po przeciwnych stronach tej prostej.
przecinają się, gdy każdy z nich przecina prostą, zawierającą drugi. Odcinek przecina prostą, gdy jego końce są po przeciwnych stronach tej prostej.
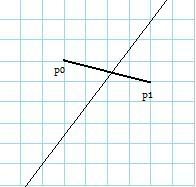
Uznamy też, że przecina on prostą, gdy jeden lub oba jego końce leżą na tej prostej:
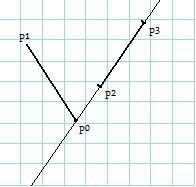
Są to niestety wspomniane "przypadki brzegowe", do których będziemy musieli podejść z wzmożoną czujnością. Okazuje się, że znów będziemy potrzebowali określić wzajemne położenie pewnych odcinków skierowanych. Weźmy przykładowe położenie dwóch odcinków:
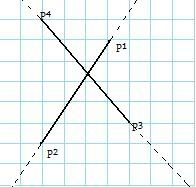
By sprawdzić po której stronie prostej zawierającej 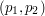 znajduje się punkt
znajduje się punkt 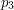 , wystarczy sprawdzić, po której stronie
, wystarczy sprawdzić, po której stronie 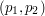 znajduje sie ten punkt. Tak samo należy uczynić dla
znajduje sie ten punkt. Tak samo należy uczynić dla 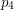 . Liczyć będziemy zatem iloczyny wektorowe
. Liczyć będziemy zatem iloczyny wektorowe 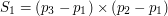 i
i 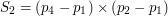 . Podobnie sytuacja wyglądać będzie dla określenia, czy
. Podobnie sytuacja wyglądać będzie dla określenia, czy 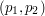 przecina prostą zawierającą
przecina prostą zawierającą 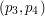 . Obliczymy iloczyny
. Obliczymy iloczyny 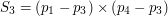 i
i 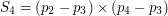
Zauważmy, że gdy 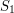 i
i 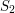 mają przeciwne znaki (żaden nie jest zerem) i sytuacja wygląda analogicznie dla
mają przeciwne znaki (żaden nie jest zerem) i sytuacja wygląda analogicznie dla 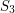 i
i 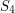 , to zachodzi sytuacja "czystego przecięcia", bez końca pewnego odcinka na drugim odcinku. Wtedy z całą mocą można stwierdzić, że odcinki przecinają się. Co jednak, gdy pewien z tych iloczynów jest równy zeru? Oznacza to, że koniec jednego z odcinków (zależny od indeksu iloczynu, np. gdy
, to zachodzi sytuacja "czystego przecięcia", bez końca pewnego odcinka na drugim odcinku. Wtedy z całą mocą można stwierdzić, że odcinki przecinają się. Co jednak, gdy pewien z tych iloczynów jest równy zeru? Oznacza to, że koniec jednego z odcinków (zależny od indeksu iloczynu, np. gdy 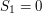 wiemy, że
wiemy, że 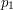 ,
,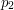 i
i 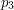 są współliniowe, więc
są współliniowe, więc 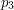 leży na prostej, zawierającej
leży na prostej, zawierającej 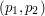 ) leży na prostej zawierającej drugi. Trzeba zatem wtedy sprawdzić, czy ten punkt leży na drugim odcinku. Jest to proste sprawdzenie - wiedząc, że punkty są współliniowe, musimy tylko zbadać, czy jedna ze współrzędnych tego punktu (np.
) leży na prostej zawierającej drugi. Trzeba zatem wtedy sprawdzić, czy ten punkt leży na drugim odcinku. Jest to proste sprawdzenie - wiedząc, że punkty są współliniowe, musimy tylko zbadać, czy jedna ze współrzędnych tego punktu (np.  ) znajduje się między odpowiadającymi współrzednymi końców tego odcinka. Dla takich odcinka
) znajduje się między odpowiadającymi współrzednymi końców tego odcinka. Dla takich odcinka 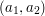 i punktu
i punktu 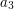 wystarczy zatem sprawdzić, czy:
wystarczy zatem sprawdzić, czy:
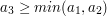 i
i 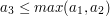 .
.
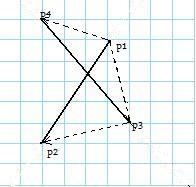
Jeżeli to sprawdzenie da odpowiedź przeczącą, nie przesądza to jeszcze o tym, że odcinki się nie przecinają. Nalezy przeprowadzić test dla wszystkich tych 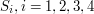 , które wyniosą zero. Poniższy przykład ilustruje, że jedno sprawdzenie nie zawsze wystarczy:
, które wyniosą zero. Poniższy przykład ilustruje, że jedno sprawdzenie nie zawsze wystarczy:
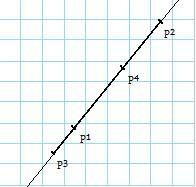
Widzimy, że przykładowe odcinki 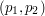 i
i 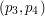 przecinają się w nieskończonej ilości punktów. Przypuśćmy, że obliczylismy
przecinają się w nieskończonej ilości punktów. Przypuśćmy, że obliczylismy 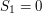 . Okazało się zatem, że przykład nie kwalifikuje się do "czystego przecięcia". Sprawdzamy więc, czy
. Okazało się zatem, że przykład nie kwalifikuje się do "czystego przecięcia". Sprawdzamy więc, czy 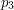 leży między
leży między 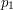 i
i 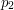 . Okazuje się, że nie. Przerywając teraz procedurę z odpowiedzią : "Nie przecinają się!", popełnilibyśmy błąd. Mamy bowiem:
. Okazuje się, że nie. Przerywając teraz procedurę z odpowiedzią : "Nie przecinają się!", popełnilibyśmy błąd. Mamy bowiem: 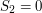 i
i 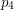 leży pomiedzy
leży pomiedzy 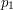 i
i 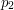 . By sformułować dokładny algorytm, zdefiniujmy w pseudokodzie funkcje:
. By sformułować dokładny algorytm, zdefiniujmy w pseudokodzie funkcje:
iloczyn(punkt p1, punkt p2, punkt p3) {
return (x2 - x1)(y3 - y1) - (x3 - x1)(y2 - y1) //zwracamy iloczyn skalarny wektorów (p2-p1) i (p3-p1)
}
lezy_miedzy(punkt p1, punkt p2, punkt p3) {
if min{x1,x2} =< x_3 =< max{x1,x2} return true //zakładamy, że p1,p2 i p3 są współliniowe
else return false
}
Wtedy możemy zdefiniować funkcję:
przecinaja_się(punkt p1, punkt p2, punkt p3, punkt p4) { //rozważamy odcinki (p1,p2) i (p3,p4)
S_1 = iloczyn(p1, p3, p2)
S_2 = iloczyn(p1, p4, p2)
S_3 = iloczyn(p3, p1, p4)
S_4 = iloczyn(p3, p2, p4)
if ((S_1 > 0 i S_2 < 0) lub (S_1 < 0 i S_2 > 0)) i ((S_3 < 0 i S_4 > 0) lub (S_3 > 0 i S_4 < 0)) return true
else if S_1 = 0 i lezy_miedzy(p1, p2, p3) return true
else if S_2 = 0 i lezy_miedzy(p1, p2, p4) return true
else if S_3 = 0 i lezy_miedzy(p3, p4, p1) return true
else if S_4 = 0 i lezy_miedzy(p3, p4, p2) return true
else return false
}
Zauważmy, że ten algorytm sprawdza zarówno, czy odcinki "przecinają się czysto", jak i czy nie zachodzi "przypadek brzegowy". Tak zdefiniowana funkcja przecinaja_sie może być bardzo przydatna przy innych algorytmach geometrycznych, na przykład takich, jak sprawdzanie, czy punkt należy do wielokąta (wypukłego bądź nie). Tyle w tym artykule. Zapraszam do robienia zadań na następnej stronie!



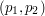 i
i 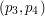 przecinają się, gdy każdy z nich przecina prostą, zawierającą drugi. Odcinek przecina prostą, gdy jego końce są po przeciwnych stronach tej prostej.
przecinają się, gdy każdy z nich przecina prostą, zawierającą drugi. Odcinek przecina prostą, gdy jego końce są po przeciwnych stronach tej prostej.


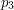 , wystarczy sprawdzić, po której stronie
, wystarczy sprawdzić, po której stronie 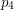 . Liczyć będziemy zatem iloczyny wektorowe
. Liczyć będziemy zatem iloczyny wektorowe 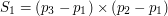 i
i 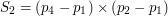 . Podobnie sytuacja wyglądać będzie dla określenia, czy
. Podobnie sytuacja wyglądać będzie dla określenia, czy 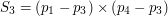 i
i 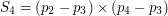

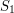 i
i 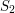 mają przeciwne znaki (żaden nie jest zerem) i sytuacja wygląda analogicznie dla
mają przeciwne znaki (żaden nie jest zerem) i sytuacja wygląda analogicznie dla 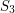 i
i 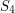 , to zachodzi sytuacja "czystego przecięcia", bez końca pewnego odcinka na drugim odcinku. Wtedy z całą mocą można stwierdzić, że odcinki przecinają się. Co jednak, gdy pewien z tych iloczynów jest równy zeru? Oznacza to, że koniec jednego z odcinków (zależny od indeksu iloczynu, np. gdy
, to zachodzi sytuacja "czystego przecięcia", bez końca pewnego odcinka na drugim odcinku. Wtedy z całą mocą można stwierdzić, że odcinki przecinają się. Co jednak, gdy pewien z tych iloczynów jest równy zeru? Oznacza to, że koniec jednego z odcinków (zależny od indeksu iloczynu, np. gdy 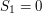 wiemy, że
wiemy, że 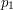 ,
,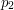 i
i 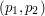 ) leży na prostej zawierającej drugi. Trzeba zatem wtedy sprawdzić, czy ten punkt leży na drugim odcinku. Jest to proste sprawdzenie - wiedząc, że punkty są współliniowe, musimy tylko zbadać, czy jedna ze współrzędnych tego punktu (np.
) leży na prostej zawierającej drugi. Trzeba zatem wtedy sprawdzić, czy ten punkt leży na drugim odcinku. Jest to proste sprawdzenie - wiedząc, że punkty są współliniowe, musimy tylko zbadać, czy jedna ze współrzędnych tego punktu (np.  ) znajduje się między odpowiadającymi współrzednymi końców tego odcinka. Dla takich odcinka
) znajduje się między odpowiadającymi współrzednymi końców tego odcinka. Dla takich odcinka 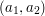 i punktu
i punktu 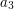 wystarczy zatem sprawdzić, czy:
wystarczy zatem sprawdzić, czy: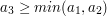 i
i 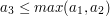 .
.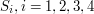 , które wyniosą zero. Poniższy przykład ilustruje, że jedno sprawdzenie nie zawsze wystarczy:
, które wyniosą zero. Poniższy przykład ilustruje, że jedno sprawdzenie nie zawsze wystarczy:
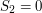 i
i 

