Warto być leniwym
08.12.2009 - Krzysztof Skrzętnicki
   List comprehensionsW poprzednim akapicie po cichu przemyciłem pewien zapis, który powinien wydać się znajomy dla wszystkich, którzy mieli do czynienia z matematyką. Chodzi mianowicie o zwięzłą notację dla list, zwaną po angielsku list comprehension.
List comprehension stanowi zapis:
Zapis ten rozumiemy dość intuicyjnie: jest to lista elementów równych
W odróżnieniu od notacji matematycznej w przypadku Haskella efektem nie jest zbiór lecz lista elementów, które na dodatek występują w określonej kolejności. Ćwiczenie (list comprehension) Korzystając z notacji dla list napisz wyrażenie, które odpowiada liście sześcianów (^3) liczb [1,9,12,612,62123]
Od jeden do nieskończoności...Jest jeszcze jeden sposób zastosowania notacji dla list. Możemy za jej pomocą definiować różnorakie ciągi. Przykładowo:
Odpowiedź ta może być szokująca dla osób, które w swoim życiu zetknęły się jedynie z językami, które nie mają mechanizmu leniwości (mówi się o nich, że są to języki gorliwe). Haskell jest jednak językiem leniwym! Jeżeli napiszemy program, który wykorzysta tylko określoną liczbę (np. 1000) elementów z danej listy, to nie potrzebujemy znać wartości pozostałych. Nasz program więc zakończy się w skończonym czasie pomimo tego, że operujemy w nim strukturami nieskończonymi! Zobaczmy to na przykładzie.
Po uruchomieniu:
Obliczonych zostało dokładnie 10 elementów z każdej listy - i nie więcej. Parę słów o funkcjach zip i take
Funkcja
zip była już omawiana wcześniej. Przypomnijmy jednak krótko, jak działa.zip operuje na dwóch listach. Jej zadaniem jest "spięcie" obydwu list w jedną listę par. Elementów na liście wyjściowej będzie dokładnie tyle ile wynosi długość krótszej z obu list. Elementy parowane są od początku list i odrzucane są takie, które nie posiadają pary. Implementacja funkcji zip wygląda następująco:
Przykładowo możemy uruchomić funkcję
zip na napisie (który jest listą znaków) i liście liczb naturalnych:
Funkcja
take jest jeszcze prostsza. Zwraca ona pierwszych n elementów listy, do której jest ona zaaplikowana. Przykład zastosowania:
Jako wynik zobaczymy:
Implementacja tej funkcji jest łatwa:
Ćwiczenie (list comp. + take) Napisz z pomocą notacji listowej listę wszystkich liczb nieparzystych. Wybierz z niej następnie pierwszych 100 elementów za pomocą funkcji
take.take 100 [1,3..] Uwaga na pułapkiTrzeba jednak wiedzieć, że leniwa ewaluacja bywa niebezpieczna. Możemy bardzo prosto napisać program, który nigdy się nie kończy. Wystarczy, że spróbujemy wyliczyć np. długość nieskończonej listy. Potrzebna nam wtedy będzie ona cała. Program potrzebować więc będzie nieskończonego czasu. Równie dobrze możemy poprosić o ostatni element nieskończonej listy albo o odwróconą listę nieskończoną. Każdy z poniższych programów nigdy nie zakończy się z sukcesem.
Co gorsza, nie tylko nie zakończą się one nigdy, ale potrafią także zużyć nieskończone zasoby pamięci! Dzieje się tak dla main2, main3 i main4. Wyjątkowo wyraźnie możemy to zobaczyć dla Wniosek: leniwość, choć przydatna, potrafi być niebezpieczna! (2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


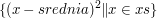
 runhaskell test8.hs
[(1,0),(2,2),(3,4),(4,6),(5,8),(6,10),(7,12),(8,14),(9,16),(10,18)]
runhaskell test8.hs
[(1,0),(2,2),(3,4),(4,6),(5,8),(6,10),(7,12),(8,14),(9,16),(10,18)]

