Warto być leniwym
08.12.2009 - Krzysztof Skrzętnicki
   Ciąg Fibonacciego : podejście pierwszeSztandarowym przykładem wykorzystania leniwości jest ciąg liczb Fibonacciego. Jest on zdefiniowany następująco: Pierwszym wyrazem jest 0. Drugim wyrazem jest 1. Każdy kolejny wyraz stanowi sumę dwóch poprzednich. Jest wiele sposobów obliczania wyrazów tego ciągu. Najbardziej naiwna implementacja, wynikająca wprost z definicji ciągu, może wyglądać następująco:
Ma ona zasadniczą wadę: obliczenie n-tego wyrazu ciągu wymaga wykładniczej liczby operacji, z których bardzo wiele wykonywanych jest kilkukrotnie. Przykładowo dla obliczenia
W każdym kolejnym kroku pojawia się coraz więcej zduplikowanych wartości. Spróbujmy więc innego podejścia, które wykorzystywać będzie leniwość Haskella. Zdefiniowaliśmy już wcześniej nieskończony ciąg liczb naturalnych. Być może uda nam się teraz zdefiniować nieskończony ciąg liczb Fibonacciego? Pożyczanie z przyszłościPowiedzieliśmy już sobie, że leniwość pozwala nam definiować wartości, które obliczone będą dopiero wtedy, gdy będą wykorzystane. Można obrócić to stwierdzenie i powiedzieć inną rzecz: możemy definiować nowe wartości przy użyciu takich, których wartości jeszcze nie znamy, pod warunkiem że później będą one znane. Brzmi trochę skomplikowanie? Zobaczmy więc przykład. Chcemy zdefiniować nieskończony ciąg naprzemiennie występujących elementów [1,2,3]. Oto jak to zrobić w Haskellu:
W momencie definiowania listy take 20 ciag1 [1,2,3,1,2,3,1,2,3,1,2,3,1,2,3,1,2,3,1,2] Ćwiczenie (take + ciag1) Myślenie o rekurencyjnej definicji ciągu
ciag1 może przegrzać szare komórki. Aby ułatwić im zadanie spróbuj pobawić się tym ciągiem za pomocą funkcji take. W poniższym polu możesz zdefiniowanych jest kilka ciągów: ciag1, ciag2, ciag3, ciag4. Spróbuj zgadnąć ich definicje.
Pójdźmy teraz krok dalej.
Ponieważ zipWith generuje elementy ciągu w sposób leniwy, możemy go wykorzystać do definiowania nieskończonych list. Możemy więc stworzyć listę kwadratów:
I taka definicja zadziała, o czym możemy się przekonać:
Ciąg Fibonacciego : tym razem szybciejMożemy już wrócić do ciągu Fibonacciego. Potrafimy już definiować ciągi przy użyciu zipWith. Wiem już także, że możemy używać wartości ciągu podczas tworzenia samej jego definicji. To wszystko pozwala nam napisać definicję tego ciągu w jednej linijce!
Zastanówmy się jak to działa. Pierwsze dwa elementy to 0 i 1 - o tym mówimy wprost. Następne elementy tworzone są jako suma sąsiednich elementów dwóch ciągów: 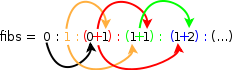
Ćwiczenie (fibs) Używając funkcji
take i zip wypisz pierwszych 20 liczb Fibonacciego wraz z ich numerami ((1,0),(2,1),(3,1),(4,2),(5,3) itd.). Lista fibs jest już zdefiniowana.
(2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




