Programowanie funkcjonalne - inne spojrzenie na świat

Ilu ludzi na świecie - tyle sposobów postrzegania tego świata. Języki programowania służą opisowi świata programów - i tutaj również zaskoczyć nas może wielka różnorodność.

Zastanówmy się czym różnią się te dwa przepisy na znalezienie długości listy elementów:

Można tak: Wyzeruj licznik. Zacznij na początku listy. Jeżeli znalazłeś się na końcu listy, zwróć licznik. W przeciwnym wypadku zwiększ licznik o jeden, przesuń się do następnego elementu i ponownie wykonaj sprawdzenie.

Albo tak: Lista pusta ma długość zero. Rozmiar listy niepustej to jeden plus rozmiar tej listy z pominięciem pierwszego elementu.

Oba są poprawne - a jednak różnią się na pewnym podstawowym poziomie. Pierwszy opis jest imperatywny - opisuje ciąg instrukcji które należy wykonać, by uzyskać pewną wartość. Drugi opis stara się w bardziej bezpośredni sposób zdefiniować czym jest ta wartość. Ten drugi opis o wiele bardziej oddaje ducha programowania funkcjonalnego.

Języków funkcjonalnych jest wiele. Jednym z ciekawszych reprezentantów tej grupy jest Haskell. To właśnie z niego będziemy dzisiaj korzystać poznając ten interesujący paradygmat programowania.

Od matematyki do programowania

Cechą Haskella, którą często podkreślają jego sympatycy, jest czytelność zapisu. Niejednokrotnie definicja matematyczna funkcji jest bardzo podobna do kodu programu.

W Haskellu funkcje działają na zasadzie rozpatrywania przypadków. Każdy z przypadków zapisujemy w formie:

1

nazwa_funkcji argument1 argument2 ... = wartość

Co oznacza rozpatrywanie przypadków? Oznacza to, że możemy nakładać pewne warunki na to, jaką wartość przyjmują poszczególne argumenty.

Aby zobaczyć, jak działa to w praktyce, rozważmy pewną bardzo prostą funkcję.

1
2

zeroJeden 0 = "zero"
zeroJeden 1 = "jeden"

I tak dla liczby  0 funkcja zwraca napis "zero", zaś dla liczby 1 - "jeden". Dociekliwy czytelnik zada pytanie: a co w pozostałych przypadkach? Okazuje się, że spowoduje to błąd i w najprostszym przypadku nasz program po prostu się zakończy.

Jak długa jest ta lista?

Wróćmy teraz do przepisu na długość funkcji z początku artykułu. Tutaj możemy przeczytać go równolegle z kodem programu, który realizuje tą funkcję:

1
2
3
4
5

dlugosc [] = 0 -- lista pusta ma długość zero
 
-- rozmiar listy niepustej to jeden plus rozmiar listy   
-- z pominięciem pierwszego elementu
dlugosc (pierwszy_element:reszta) = 1 + dlugosc reszta 

Wyjaśnijmy sobie szczegóły tego zapisu.

W przypadku funkcji dlugosc pierwszy przypadek:

1

dlugosc [] = 0

Drugi przypadek wprowadza nam sposób na dopasowywanie argumentu do listy niepustej. Jak można się domyśleć przed dwukropkiem : znajduje się pierwszy element na liście, zwany popularnie głową (ang. head). Po dwukropku znajduje się cała reszta listy, zwana ogonem (ang. tail). Tak więc jeżeli mamy:

1

(pierwszy_element : reszta) = [1,2,3,4,5]

To pierwszy_element równy jest 1, zaś reszta równa jest [2,3,4,5].

Wracając więc do naszej funkcji: w drugim przypadku wywołujemy więc rekurencyjnie funkcję dlugosc na ogonie listy reszta i zwracamy wartość o 1 większą.

Małe ćwiczenie. W poniższe pole możesz wpisać kod do wykonania. Spróbuj wpisać np.:

1

dlugosc [1,2,3]

albo:

1

dlugosc "Hello world!"

---

Istnieją dwa sposoby zapisu list. W obu z nich listę pustą oznacza się przez []. Różnią się w odniesieniu do list dłuższych. Oto pierwszy z nich:

1	[1,2,3,4,5]

Jego zaletą jest czytelność. Wadą - to, że z góry musimy powiedzieć, jakiej długości jest lista. Ponieważ nasza funkcja dlugosc ma działać dla list o dowolnej długości, nie możemy użyć tego zapisu.

Na scenę wkracza więc drugi sposób zapisu. Zamiast podawać wszystkie elementy po kolei mówimy tylko, że lista to coś, co ma pierwszy element (głowę) i wszystkie pozostałe (ogon). Głowę oddzielamy od ogona dwukropkiem:

1	głowa : ogon

Zapis powyższej listy wyglądałby więc następująco:

1	1:(2:(3:(4:(5:[]))))

Dla czytelności zapisu poszczególne fragmenty zostały otoczone nawiasami. Można je jednak pominąć:

1	1:2:3:4:5:[]

Każdy z dwukropktów w powyższym zapisie można odczytać jako "...jest głową, a ogonem jest lista taka że...".

1 2 3 4 5

1 jest głową, a ogonem jest lista taka że     (2 jest głową, a ogonem jest lista taka że     (3 jest głową, a ogonem jest lista taka że     (4 jest głową, a ogonem jest lista taka że     (5 jest głową, a ogonem jest lista []))))

Listę tą można także zwizualizować tym diagramem:

---

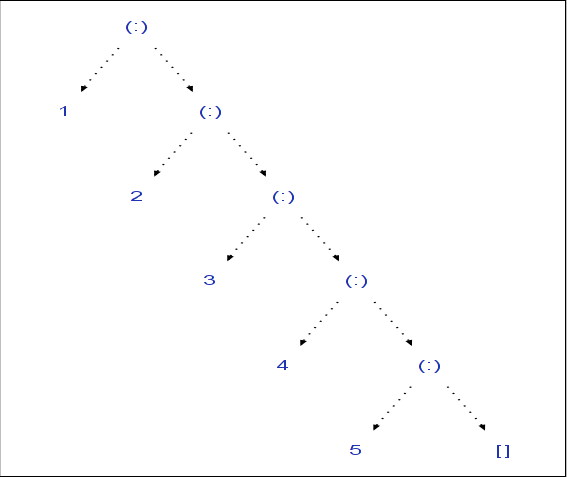
A po co mi ten kaktus?

Zagłębijmy się dalej w ten język programowania. Zdarza się, że pewna część wartości nas nie interesuje. Tak jest w przypadku głowy listy w funkcji dlugosc:

1

dlugosc (pierwszy_element:reszta) = 1 + dlugosc reszta

pierwszy_element nie jest nigdzie używany po prawej stronie równania! Zamiast więc wymyślać niepotrzebne nikomu nazwy możemy użyć wygodnego mechanizmu.

Wystarczy, że zamiast nazwy zmiennej wpiszemy znak podkreślenia: _. Używamy go wtedy, gdy nie interesuje nas dana wartość. Dzięki temu podkreślamy co jest ważne w funkcji i zasługuje na nazwę, a co możemy pominąć. Zyskujemy dzięki temu na czytelności zapisu. Poprawiony kod prezentuje się następująco:

1
2
3
4
5

dlugosc [] = 0 -- lista pusta ma długość zero
 
-- rozmiar listy niepustej to jeden plus rozmiar listy   
-- z pominięciem pierwszego elementu
dlugosc (_:reszta) = 1 + dlugosc reszta 

Zabawy listami

1. Funkcja dodająca element do listy dwa razy

1	dodajDwa x xs = (x:x:xs)

Funkcja dodajDwa pobiera dwa argumenty: element x i listę xs. Następnie tworzy nową listę której pierwsze dwa elementy równe są x, zaś całą resztę stanowi xs.

Tutaj widzimy jeszcze jedną ciekawą właściwość. Kiedy zapis x:xs występował po lewej stronie równania funkcji lista była "rozbierana" - dekonstruowana. Ten sam zapis po prawej stronie oznacza tworzenie nowej wartości, czyli konstruowanie. Tak więc w dokładnie ten sam sposób, w który wcześniej dopasowywaliśmy listę do wzorca, możemy teraz zbudować nową. Nie jest to przypadek: właściwość ta jest prawdziwa dla wszystkich struktur danych w Haskellu.

Ćwiczenie. Jakie argumenty należy podać do dodajDwa, aby wynikiem było [4,4,2,3]? Odpowiedź wpisz poniżej.

2. Dla ćwiczenia napiszmy teraz funkcję, która potraja wartość pierwszej liczby na liście:

1	razyTrzy (x:xs) = ((x*3):xs)

Podobnie jak w poprzednich funkcjach rozkładamy listę na głowę x i ogon xs, a następnie tworzymy nową listę o głowie x*3 i ogonie xs.

Ćwiczenie. Obliczamy wartość

1	razyTrzy (dodajDwa x xs)

Podaj wartość x xs, tak by w wyniku otrzymać [6,2,0]