Zasada włączeń i wyłączeń
02.12.2009 - Krzysztof Piecuch
  PodzielnośćLimit czasowy: 1s; Limit pamieciowy: 32MB; Zadanie polega na obliczeniu ile jest liczb w danym przedziale, które są podzielne przez którąś z określonych liczb. Wejście Pierwsza linia wejścia określa trzy liczby całkowity A, B oraz N. Ostatnie dwie określają przedział w którym będziemy szukali liczb ( Wyjście Na standardowe wyjście należy wypisać ile liczb naturalnych z przedziału Przykład Dla danych wejściowych: 3 1 10000 Poprawną odpowiedzią jest: 2333 Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
ProstopadłościanyLimit czasowy: 5s; Limit pamięciowy: 32MB; Dla danych N prostopadłościanów policzyć objętość powstałą po sklejeniu ich razem. Dane wejściowe W pierwszym wierszu znajduje się liczba N, określająca ilość prostopadłościanów ( Dane wyjściowe Objętość bryły. Przykład Dla danych wejściowych 2 Poprawną odpowiedzią jest: 15 Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto.
Dla osób bardzo ambitnych cytuję zadanie z potyczek algorytmicznych: PodróżLimit czasowy: 5s; Limit pamięciowy: 32MB; Potyczki algorytmiczne 2008 W Bajtocji znajduje sie n miast ponumerowanych od 1 do n. Miasta te są połączone siecią m dróg dwukierunkowych. Wiadomo, że każda para miast jest połączona za pomocą co najwyżej jednej drogi.
Nie możesz wysyłać i oglądać rozwiązań tego zadania ponieważ nie jesteś zalogowany. Zaloguj się lub załóż konto. (4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


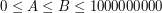 ). W kolejnych N (
). W kolejnych N (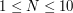 ) wierszach znajdują się liczby
) wierszach znajdują się liczby 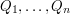 .
.![$ [A, B] $](/files/tex/fc220b6366001ab2f4e89921fc10fbab9936845e.png) jest podzielnych przez którąś z liczb
jest podzielnych przez którąś z liczb 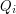 .
.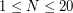 ). W kolejnych N wierszach znajduje się 6 liczb całkowitych x1, y1, z1, x2, y2, z2 określające przeciwległe wierzchołki prostopadłościanu przy czym:
). W kolejnych N wierszach znajduje się 6 liczb całkowitych x1, y1, z1, x2, y2, z2 określające przeciwległe wierzchołki prostopadłościanu przy czym: 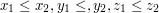 oraz
oraz 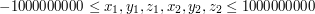 .
.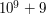 .
.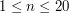 ,
, 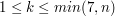 ,
, 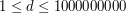 ) pooddzielane pojedynczymi odstępami. Kolejne m wierszy zawiera opisy połączeń między miastami Bajtocji. Opis drogi składa się z dwóch liczb
) pooddzielane pojedynczymi odstępami. Kolejne m wierszy zawiera opisy połączeń między miastami Bajtocji. Opis drogi składa się z dwóch liczb 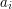 ,
, 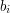 (
(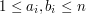 ,
, 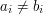 ), oddzielonych pojedynczym odstępem i oznaczających numery miastpołączonych za pomocą i-tej drogi.
), oddzielonych pojedynczym odstępem i oznaczających numery miastpołączonych za pomocą i-tej drogi.

