Zasada włączeń i wyłączeń
02.12.2009 - Krzysztof Piecuch
  Teraz przedstawimy kilka przykładów ilustrujących zastosowanie metody włączeń i wyłączeń. PrzykładyRozważmy następujący problem: chcemy znaleźć ilość wszystkich liczb naturalnych mniejszych lub równych 10000, które są podzielne przez 6, 15 lub 20. Łatwo policzyć ile w tym przedziale jest liczb podzielnych przez 6. Jest ich Spróbujmy policzyć ten problem z metody włączeń i wyłączeń. Oznaczmy przez
Kolejnym zadaniem jakim się zajmiemy jest policzenie objętości bryły powstałej przez sklejenie kilku prostopadłościanów. Mamy dane dziesięć prostopadłościanów o krawędziach równoległych do odpowiednich osi układu współrzędnych. Prostopadłościan jest dany za pomocą współrzędnych dolnego, lewego, przedniego rogu Jednak suma dwóch (albo dziesięciu) prostopadłościanów może być bryła mniej regularną i znalezienie wzoru na jego objętość może być rzeczą niebanalną. Jednak przecięcie dwóch prostopadłościanów (jeśli jest niepuste) jest również prostopadłościanem. Powiem więcej - znalezienie współrzędnych wierzchołków przecięcia jest stosunkowo prostym zadaniem. Zostawimy to jako ćwiczenie. Złożoność i implementacjaSporą wadą metody jest złożoność. Gdy chcemy policzyć sumę n zbiorów: Zastanówmy się teraz jaka jest różnica między algorytmem wykonującym (4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


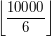 . Łatwo też policzyć ile jest liczb w tym przedziale które są zarówno podzielne przez 6 jak i przez 15. Jest ich
. Łatwo też policzyć ile jest liczb w tym przedziale które są zarówno podzielne przez 6 jak i przez 15. Jest ich 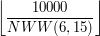 . Jednak policzenie ile jest liczb, które są podzielne przez 6 lub przez 15... już takie łatwe nie jest.
. Jednak policzenie ile jest liczb, które są podzielne przez 6 lub przez 15... już takie łatwe nie jest. 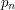 zbiór liczb z naszego przedziału podzielne przez
zbiór liczb z naszego przedziału podzielne przez  . Wtedy:
. Wtedy: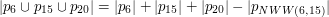
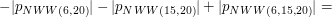
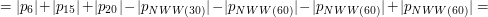
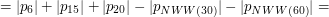
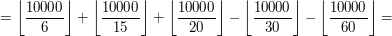
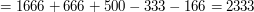
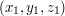 i górnego, prawego, tylniego rogu
i górnego, prawego, tylniego rogu 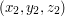 . Istnieje prosty wzór na objętość takiego prostopadłościanu.
. Istnieje prosty wzór na objętość takiego prostopadłościanu. 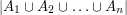 potrzebujemy policzyć aż
potrzebujemy policzyć aż 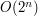 różnych przecięć. Gdy
różnych przecięć. Gdy 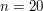 mamy 1048575 podzbiorów - czyli mniej więcej tyle ile jesteśmy w stanie w limicie czasowym przetworzyć. Na przykład dla
mamy 1048575 podzbiorów - czyli mniej więcej tyle ile jesteśmy w stanie w limicie czasowym przetworzyć. Na przykład dla 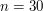 mamy już ponad miliard różnych przecięć. Jest to zdecydowanie za dużo.
mamy już ponad miliard różnych przecięć. Jest to zdecydowanie za dużo.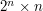 operacji, a algorytmem wykonującym
operacji, a algorytmem wykonującym 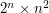 operacji. Z jednej strony może się wydawać, że niewielka bo
operacji. Z jednej strony może się wydawać, że niewielka bo 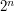 jest na tyle duże, że czynnik
jest na tyle duże, że czynnik 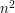 wydaje się pomijalny dla odpowiednio dużych
wydaje się pomijalny dla odpowiednio dużych 

