Teraz postarajmy się zaimplementować ogólną metodę włączeń i wyłączeń. Powiedzmy, że mamy zaimplementowaną funkcję 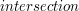 , która jako argumenty potrzebuje tablicę wartości logicznych
, która jako argumenty potrzebuje tablicę wartości logicznych  oraz jej długość
oraz jej długość 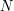 . Liczy ona ilość elementów dla przecięcia pewnych zbiorów. Mówiąc konkretniej to bierze on zbiór
. Liczy ona ilość elementów dla przecięcia pewnych zbiorów. Mówiąc konkretniej to bierze on zbiór  -ty jeśli wartość tablicy
-ty jeśli wartość tablicy ![$ A\left[i-1 \right] $](/files/tex/04e0d52c0308e75497199d260123dd31769aa4e1.png) jest ustawiona na prawdę. Czyli na przykład
jest ustawiona na prawdę. Czyli na przykład ![$ intersection\left(\left[0, 1, 1, 0, 1\right], 5\right) $](/files/tex/d9662474a54737ff982569a4c0728dc714bd9aad.png) wyznacza ilość elementów w zbiorze
wyznacza ilość elementów w zbiorze 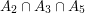 .
.
Oznaczmy na chwilę prawdę jako jeden, a fałsz jako zero. Tablicę A będziemy "zwiększać o 1" tak jakgdyby była ona licznikiem binarnym. To znaczy, że dla 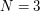 będzie ona przyjmowała następujące wartości:
będzie ona przyjmowała następujące wartości:
A = [1, 0 ,0];
A = [0, 1, 0];
A = [1, 1, 0];
A = [0, 0, 1];
A = [1, 0, 1];
A = [0, 1, 1];
A = [1, 1, 1];
Czytając te cyfry od prawej do lewej otrzymujemy kolejne liczby naturalne w systemie dwójkowym. 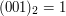 ,
, 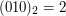 ,
, 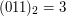 i tak dalej.
i tak dalej.
W naszym rozwiązaniu pojawiają się ponadto zmienna answer oraz sign. Każdy kto zna dobrze angielski od razu zgadnie, że w zmiennej answer będziemy trzymali obliczoną odpowiedź, a w zmiennej sign znak 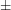 w zależności od tego czy ilość elementów danego przecięcia będziemy chcieli dodać czy odjąć.
w zależności od tego czy ilość elementów danego przecięcia będziemy chcieli dodać czy odjąć.
int sum(int N)
{
int answer = 0;
int sign = 1;
bool *A = new bool[N+1];
A[0] = true;
for (int i = 1; i <= N; i++)
A[i] = false;
while (A[N] == 0)
{
answer += sign * intersection(A, N);
int j = 0;
while (A[j])
{
A[j] = false;
sign = -sign;
j++;
}
A[j] = true;
sign = -sign;
}
return answer;
}
Po deklaracji zmiennych, ustawiamy wartości początkowe tablicy  . Następnie w pętli najpierw aktualizujemy wynik, a następnie zwiększamy licznik tablicy
. Następnie w pętli najpierw aktualizujemy wynik, a następnie zwiększamy licznik tablicy  . Robimy to w ten sposób, że zerujemy od lewej wszystkie
. Robimy to w ten sposób, że zerujemy od lewej wszystkie  , aż natrafimy na pierwsze
, aż natrafimy na pierwsze  z lewej. Następnie to
z lewej. Następnie to  zamieniamy na
zamieniamy na  . Zmieniamy znak za każdym razem gdy zmieniamy jakąś jedynkę na zero lub zero na jedynkę.
. Zmieniamy znak za każdym razem gdy zmieniamy jakąś jedynkę na zero lub zero na jedynkę.
Wyjaśnienia może wymagać jeszcze fakt, że tablica  ma o jeden element więcej niż potrzeba. Jest tak tylko na użytek tej funkcji. Funkcja intersection widzi już tą tablicę w "zwykłej" wielkości, dzięki zmiennej N. Już wyjaśniam czemu służy dodatkowa komórka. Gdy
ma o jeden element więcej niż potrzeba. Jest tak tylko na użytek tej funkcji. Funkcja intersection widzi już tą tablicę w "zwykłej" wielkości, dzięki zmiennej N. Już wyjaśniam czemu służy dodatkowa komórka. Gdy 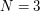 ostatnie przecięcie jakie sprawdzamy jest określone w tablicy jako
ostatnie przecięcie jakie sprawdzamy jest określone w tablicy jako ![$ \left[1, 1, 1, 0]\right $](/files/tex/4478626d89180918ac0e5f08fe66a7c01b4b9eeb.png) . Ostatnie zero jest właśnie tą dodaną komórką. Jak teraz będziemy próbowali zwiększyć o
. Ostatnie zero jest właśnie tą dodaną komórką. Jak teraz będziemy próbowali zwiększyć o  taki licznik otrzymamy
taki licznik otrzymamy ![$ \left[0, 0, 0, 1\right] $](/files/tex/40e65b86c2f15407611685521ef7f3c44898bf03.png) . Dzięki temu mamły prosty warunek końca pętli while. Działamy w pętli tak długo jak długo dodatkowa komórka jest ustawiona na zero.
. Dzięki temu mamły prosty warunek końca pętli while. Działamy w pętli tak długo jak długo dodatkowa komórka jest ustawiona na zero.
Zadania
Do implementacji pozostają zadania przedstawione w treści artykułu. Implementacja ich powinna być ciekawym problemem samym w sobie. Zapraszam na następną stronę wszystkich chcących się zmierzyć z zadaniami!




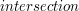 , która jako argumenty potrzebuje tablicę wartości logicznych
, która jako argumenty potrzebuje tablicę wartości logicznych  oraz jej długość
oraz jej długość 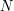 . Liczy ona ilość elementów dla przecięcia pewnych zbiorów. Mówiąc konkretniej to bierze on zbiór
. Liczy ona ilość elementów dla przecięcia pewnych zbiorów. Mówiąc konkretniej to bierze on zbiór  -ty jeśli wartość tablicy
-ty jeśli wartość tablicy ![$ A\left[i-1 \right] $](/files/tex/04e0d52c0308e75497199d260123dd31769aa4e1.png) jest ustawiona na prawdę. Czyli na przykład
jest ustawiona na prawdę. Czyli na przykład ![$ intersection\left(\left[0, 1, 1, 0, 1\right], 5\right) $](/files/tex/d9662474a54737ff982569a4c0728dc714bd9aad.png) wyznacza ilość elementów w zbiorze
wyznacza ilość elementów w zbiorze 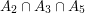 .
.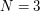 będzie ona przyjmowała następujące wartości:
będzie ona przyjmowała następujące wartości: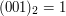 ,
, 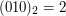 ,
, 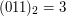 i tak dalej.
i tak dalej.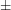 w zależności od tego czy ilość elementów danego przecięcia będziemy chcieli dodać czy odjąć.
w zależności od tego czy ilość elementów danego przecięcia będziemy chcieli dodać czy odjąć. , aż natrafimy na pierwsze
, aż natrafimy na pierwsze  z lewej. Następnie to
z lewej. Następnie to ![$ \left[1, 1, 1, 0]\right $](/files/tex/4478626d89180918ac0e5f08fe66a7c01b4b9eeb.png) . Ostatnie zero jest właśnie tą dodaną komórką. Jak teraz będziemy próbowali zwiększyć o
. Ostatnie zero jest właśnie tą dodaną komórką. Jak teraz będziemy próbowali zwiększyć o ![$ \left[0, 0, 0, 1\right] $](/files/tex/40e65b86c2f15407611685521ef7f3c44898bf03.png) . Dzięki temu mamły prosty warunek końca pętli while. Działamy w pętli tak długo jak długo dodatkowa komórka jest ustawiona na zero.
. Dzięki temu mamły prosty warunek końca pętli while. Działamy w pętli tak długo jak długo dodatkowa komórka jest ustawiona na zero.

