Kopiec (binarny)
30.11.2009 - Michał Karpiński
 Czym jest kopiec ?Zanim odpowiem na to pytanie najpierw powinieneś poznać kilka nowych pojęć związanych z kopcami: 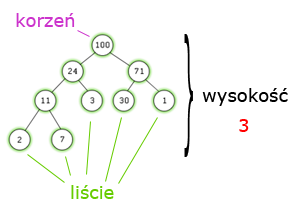
Przedstawię teraz najkrótszą znaną mi definicję kopca: „kopiec jest to drzewiasta struktura danych, która spełnia własność kopca”. Oznacza to, że wartości potomków węzła są w stałej relacji z wartością rodzica. Istnieją bowiem dwie ważne odmiany kopców: kopce typu max i kopce typu min. W obydwu przypadkach wartości w węzłach spełniają własność kopca zależną od typu kopca:
Oczywiście własności te zachodzą dla wszystkich węzłów poza korzeniem (ponieważ korzeń nie ma rodzica). Poniżej znajduje się przykład reprezentacji kopca typu max w postaci drzewa binarnego oraz tablicy. Zauważ, że ponumerowaliśmy wszystkie węzły od lewej do prawej tak, żeby liczba nad węzłem w kopcu odpowiadała indeksowi w tablicy. Linie łączące elementy w tablicy przedstawiają relację rodzic-potomek. 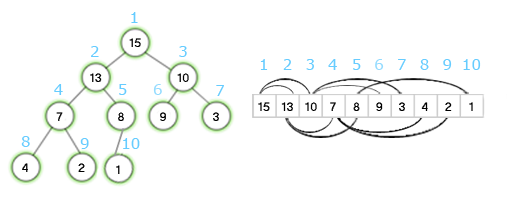 Patrząc na rysunek nie trudno się domyśleć jak wyglądają procedury znajdowania indeksu rodzica oraz lewego i prawego potomka:
Proste ćwiczenieCzy ciąg [23,17,14,6,13,10,1,5,4,12] jest kopcem typu max? Aby rozwiązać to zadanie należy znaleźć wszystkie krawędzie łączące węzły z ich potomkami sprawdzając przy okazji czy relacja między rodzicem a potomkiem spełnia własność kopca typu max. 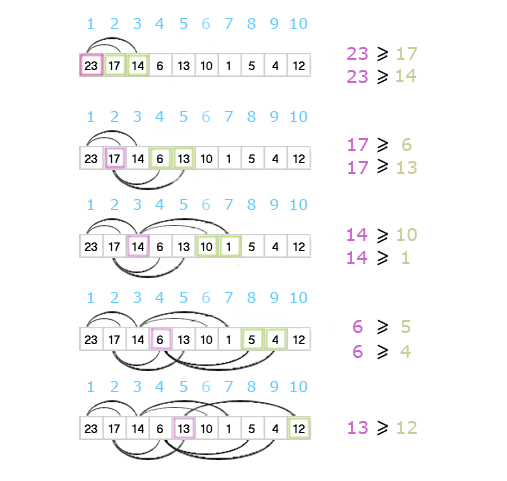 Okazuje się, że podany ciąg jest kopcem typu max. Ilustracja w postaci drzewa: 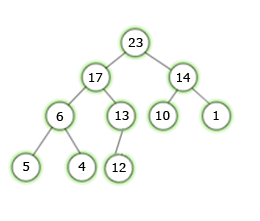 (4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




