Kopiec (binarny)
30.11.2009 - Michał Karpiński
 Sortowanie przez kopcowanieAlgorytm HEAPSORT( A ) (gdzie A jest dowolną tablicą o rozmiarze n) jest to połączenie dwóch poprzednio poznanych procedur. Algorytm rozpoczyna działanie, używając procedury BUDUJ-KOPIEC-MAX( A ) do skonstruowania kopca typu max. Wiemy, że w korzeniu tego kopca znajduje się element o największej wartości. Jedyne co trzeba zrobić to zamienić miejscami pierwszy i ostatni element tablicy A ( czyli A[1] i A[n] ) i następnie zmniejszyć rozmiar kopca o 1. Po takim zabiegu otrzymujemy tablicę A[1...(n-1)]. Zauważmy, że wszystkie węzły - oprócz pierwszego elementu - dalej spełniają własność kopca, więc aby znów uzyskać kopiec typu max, wywołujemy KOPCUJ-MAX( A, 1 ). Iterując po tablicy A zamieniamy kolejne elementy dopóki kopiec nie osiągnie rozmiaru 1. Ostatecznie otrzymujemy posortowaną rosnąco tablicę A.  Czas algorytmu wynosi O(n log n), gdyż budowanie kopca zajmuje czas O(n), a każde wywołanie KOPCUJ-MAX( A, i ) zajmuje O(log n). Uwaga: HEAPSORT jest bardzo dobrym algorytmem, ale w praktyce na ogół lepszy jest QUICKSORT. Więcej o „szybkim sortowaniu” znajdziesz tutaj. Co możemy zrobić z kopcem ?Pamiętasz jeszcze historyjkę o firmie kurierskiej? Celem Witka było zastosowanie takiej struktury danych, z której łatwo wyciągnąć element najmniejszy i przy okazji niskim kosztem dołączać nowe elementy. Wiemy już czym jest kopiec i potrafimy go zbudować, ale żeby Witek mógł usuwać i dodawać paczki trzeba dodać do naszej struktury kilka dodatkowych procedur.

Najprostszą z powyższych operacji jest MINIMUM(A), który działając na kopcu typu min zwraca wartość jego pierwszego elementu. Analogicznie działa procedura MAXIMUM(A) dla kopca typu max. Troszkę bardziej skomplikowana jest operacja usunięcia pierwszego elementu. Łatwo można usunąć korzeń, ale gdy to zrobimy, to w miejscu korzenia będzie luka i naszym zadaniem jest tą lukę wypełnić. Najrozsądniej jest wstawić w to miejsce ostatni element kopca, ale teraz jest prawie pewne, że nie spełnia on własności kopca. Wszystkie inne węzły pozostają na swoim miejscu, czyli mamy kopiec, w którym tylko jeden węzeł nie spełnia własności kopca. Chyba już się domyślasz, jaką procedurę należy zastosować?  Oto przykład działania operacji usunięcia elementu z kopca: 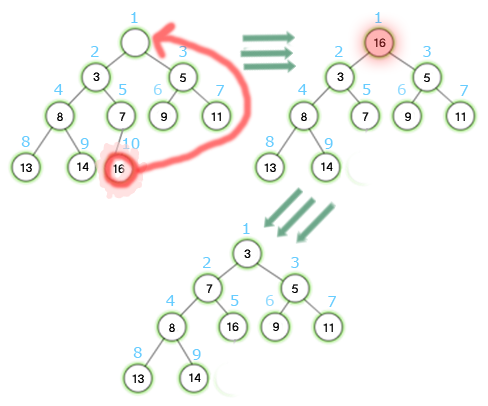 Usunięcie pierwszego elementu z kopca działa w czasie O(log n). (4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




