Kopiec (binarny)
30.11.2009 - Michał Karpiński
 Budowanie kopcaW tym rozdziale pokażę jak z nieposortowanej tablicy stworzyć kopiec typu max. Pomocna w tym będzie procedura KOPCUJ-MAX(A,i) poznana w poprzednim rozdziale. Oczywistym jest, że aby zbudować kopiec, należy wywołać procedurę KOPCUJ-MAX(A,i) na każdym elemencie tablicy, ale wybór elementów, którym przywrócimy własność kopca nie jest przypadkowy. Wiemy z poprzedniego działu, że procedurę KOPCUJ-MAX(A,i) możemy wywołać tylko na kopcu, w którym jedynym elementem niespełniającym własności kopca jest i. Ten warunek zabrania nam na przywracanie własności kopca dla dowolnych elementów nieposortowanej tablicy. Zauważmy jednak, iż każdy liść kopca, jest jednocześnie 1-elementowym kopcem. Czy już widzisz rozwiązanie?  Z powyższej definicji odczytujemy, że budowanie kopca zaczynamy „od dołu”. Przykład działania procedury BUDUJ-KOPIEC-MAX(A) dla A = [4,1,3,2,15,9,10,13,7,8] widać na poniższym rysunku: 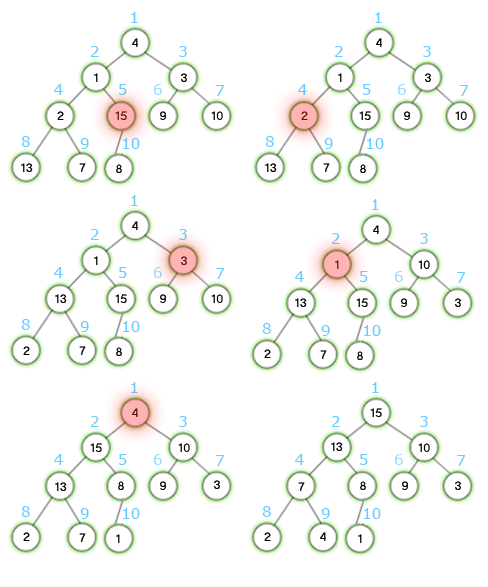 Czas budowania kopcaWiemy z poprzedniego rozdziału, że procedura KOPCUJ-MAX(A,i) działa w czasie O(log n). W procedurze BUDUJ-KOPIEC-MAX(A) wywołujemy przywracamy własność kopca n razy. W takim razie intuicja podpowiada nam, że czas budowania kopca to O(n log n). To ograniczenie jest poprawne, ale niedokładne. Można uzyskać lepsze ograniczenie. Wystarczy zauważyć, że czas działania KOPCUJ-MAX(A,i) w węźle zależy od wysokości tego węzła, a wysokości większości węzłów są małe. Czyli w n-elementowym kopcu o wysokości floor( log n ) znajduje się co najwyżej ceil(n/2^(h+1)) węzłów wysokości h. 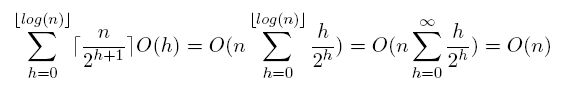 Wiem, że ten dowód może wydawać się skomplikowany i nie wymagam od Ciebie pełnego zrozumienia powyższych przekształceń. Jedyne co musisz wiedzieć to fakt, że budowanie kopca działa w liniowym czasie O(n). (4 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com




