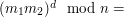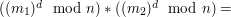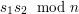"Alicjo, czy to naprawdę Ty?" , albo o podpisach cyfrowych.
29.11.2009 - Agata Murawska
  Kryptografia z wykorzystaniem algorytmu RSA
Ważnym dla nas przykładem kryptografii z kluczem publicznym jest algorytm RSA. Jego bezpieczeństwo opiera się na założeniu, że dla dużej liczby, znalezienie jej rozkładu na czynniki pierwsze jest trudne. Pary kluczy w RSA znajduje się w następujący sposób:
Dlaczego mówimy, że RSA jest bezpieczne, jeśli problem faktoryzacji (czyli rozkładu na czynniki pierwsze) jest trudny?
Jeśli znamy  i i  , to znaleźć , to znaleźć 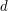 jest łatwo, pod warunkiem, że zna się rozkład jest łatwo, pod warunkiem, że zna się rozkład  na czynniki pierwsze - wtedy możemy, tak jak przy generowaniu pary kluczy, użyć rozszerzonego algorytmu Euklidesa do znalezienia na czynniki pierwsze - wtedy możemy, tak jak przy generowaniu pary kluczy, użyć rozszerzonego algorytmu Euklidesa do znalezienia 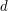 i odszyfrowywać wiadomości nieprzeznaczone dla nas. i odszyfrowywać wiadomości nieprzeznaczone dla nas. Na szczęście znalezienie dwóch naprawdę dużych liczb pierwszych wydaje się być znacznie prostsze, niż znalezienie rozkładu ich iloczynu.
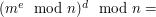 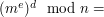 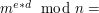 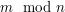
Oczywiście, jeśli wiadomość  jest długa, to trzeba ją podzielić na bloki krótsze, niż jest długa, to trzeba ją podzielić na bloki krótsze, niż  . .
Podpisy z kryptografią asymetryczną
Bogatsza o tę wiedzę Alicja zastanawia się dalej. A gdyby tak napisać wiadomość dla Boba i zaszyfrować ją swoim kluczem prywatnym? Wtedy on mógłby użyć pasującego klucza publicznego i stwierdzić, że to na pewno ona jest autorką! Możemy tak zrobić, jeśli algorytmy szyfrowania i deszyfrowania są symetryczne - ale jeśli używamy RSA, to tak właśnie jest, bo przecież
Czy ta metoda ma jakieś wady? Oczywiście! Podpis jest tak długi, jak wiadomość, którą podpisujemy. Możemy oczywiście wysłać, oprócz podpisanej wiadomości, także jej jawny odpowiednik, ale weryfikacja tożsamości autora nadal będzie wymagać wiele obliczeń, a dodatkowo podwoimy ilość wysyłanych danych. Będziemy wtedy musieli też sprawdzać, czy wiadomość po deszyfrowaniu odpowiada wiadomości niezaszyfrowanej. Wydaje się, że to trochę za dużo zachodu, prawda? Zastanówmy się jeszcze, czy wymagane na początku własności, dotyczące podpisów cyfrowych, są spełnione:
(5 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


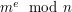 , gdzie
, gdzie 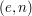 jest kluczem publicznym odbiorcy, to odszyfrowanie wiadomości polega na podniesieniu jej do odpowiedniej potęgi
jest kluczem publicznym odbiorcy, to odszyfrowanie wiadomości polega na podniesieniu jej do odpowiedniej potęgi 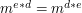 .
.

 taki, że jego odkodowanie przy pomocy klucza publicznego Alicji daje sensowną wiadomość
taki, że jego odkodowanie przy pomocy klucza publicznego Alicji daje sensowną wiadomość 
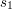 i
i 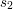 są podpisami pod wiadomościami, odpowiednio,
są podpisami pod wiadomościami, odpowiednio, 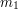 i
i 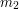
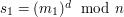 ,
, 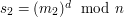 )
)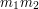 jest
jest