Sito Eratostenesa
27.11.2009 - Anna Piekarska
 Już starożytni Grecy zastanawiali się nad zagadnieniem liczb pierwszych. Aktualnie problem zdaje się wciąż nie być dostatecznie zbadany. Jednak dziś wiemy nieco więcej niż kiedyś. Do rozwoju teorii przyczynił się zdecydowanie Eratostenes - wymyślił tzw. Sito Eratostenesa czyli dość prosty algorytm znajdowania liczb pierwszych. Prosty oczywiście dla małych liczb. Wciąż nie znamy algorytmu wielomianowego na faktoryzację. Moim zdaniem na jednymi z ważniejszych późniejszych odkryć są szczególne rodzaje liczb pierwszych - np. Fermata czy Mersenne'a oraz probabilistyczne testy pierwszości. Czego się nauczymy?Dowiemy się jak sprawdzić, czy liczba jest pierwsza. Znajdziemy dzielniki pierwsze liczby, czyli dokonamy faktoryzacji. Poznamy powody, dla których liczby pierwsze są tak ważne. Zapoznamy się ze szkicem rozwiązania zadania "Najdzielniejszy dzielnik" z tegorocznej Olimpiady Informatycznej. Sposób naiwnyChcemy dowiedzieć się, czy liczba n jest pierwsza. Czemu w takim razie nie sprawdzić po prostu dla dużej ilości liczb czy są dzielnikami n? Tylko które liczby sprawdzić? Czy 15 może być dzielnikiem 10? Dlaczego?
bool isPrime(int n)
{
for(int d = 2; d < n; d++) // sprawdzamy każdy dzielnik
{
if(n % d == 0) // sprawdzamy, czy n dzieli się przez d
{
cout << d << "jest dzielnikiem " << n;
cout << ", więc " << n << " nie jest pierwsze" << endl;
return 0; // jeśli tak, to n nie jest pierwsza
}
}
return 1; // n jest pierwsza
}
PrzyspieszamyOszacujmy złożoność tego algorytmu. Pętlę wykonujemy n razy. W pętli wykonujemy stałą liczbę operacji, więc złożoność wynosi 2 jest dzielnikiem 24, więc 24 nie jest pierwsze 3 jest dzielnikiem 24, więc 24 nie jest pierwsze 4 jest dzielnikiem 24, więc 24 nie jest pierwsze 6 jest dzielnikiem 24, więc 24 nie jest pierwsze 8 jest dzielnikiem 24, więc 24 nie jest pierwsze 12 jest dzielnikiem 24, więc 24 nie jest pierwsze Czy na pewno musimy sprawdzać liczbę 12? Przecież skoro 2 dzieli 24 to
bool isPrime(int n)
{
for(int d = 2; d*d <= n; d++)
// sprawdzamy każdy dzielnik do pierwiastka
{
if(n % d == 0)
// sprawdzamy, czy n dzieli się przez d
{
cout << d << "jest dzielnikiem " << n;
cout << ", więc " << n << " nie jest pierwsze" << endl;
return 0; // jeśli tak, to n nie jest pierwsza
}
}
return 1; // n jest pierwsza
}Jaka złożoność jest teraz? Tym razem pętlę wykonujemy Więcej zapytańA co jeśli dostaniemy więcej zapytań? Powiedzmy milion. Załóżmy, że nasze zapytania też są w okolicach miliona. Wykonując za każdym razem nasz algorytm, wykonamy około Przykładowo załóżmy
const int MAX = 1000010; // tyle liczb chcemy sprawdzić
bool p[MAX]; // tablica, w której zaznaczamy, czy liczba jest pierwsza
void init()
{
for(int i = 2; i < MAX; i++) p[i] = 1;
// na początku wszystkie liczby są pierwsze
for(int i = 2; i*i < MAX; i++)
{
if(p[i])
{
for(int j = 2; i * j < MAX; j++) p[i*j] = 0;
// i*j jest wielokrotnością i, więc jest liczbą złożoną
}
}
}
Dlaczego to działa?Oczywistym jest, że żadna liczba pierwsza nie została oznaczona jako złożona. Zastanówmy się, czy może istnieć taka liczba złożona, która nie została znaleziona. Jeśli udowodnimy, że nie ma takiej, będzie to oznaczało, że algorytm jest poprawny. Załóżmy nie wprost, że pewna liczba postaci Jednak wszystkie liczby postaci Czy to działa szybciej?Musimy policzyć, jak szybko działa nasz algorytm. W końcu po co nam skomplikowany algorytm wolniejszy od tego prostego, który już znamy.
(9 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


![$ [2,n-1] $](/files/tex/9df47da76f07f57ff027488446d530b2c060e164.png) :
: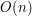 . Trochę wolno. Czy możemy to przyspieszyć?
. Trochę wolno. Czy możemy to przyspieszyć?
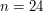 .
.
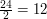 też.
też.
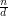 też. W takim razie każdemu dzielnikowi z przedziału
też. W takim razie każdemu dzielnikowi z przedziału ![$ [\sqrt{n},n] $](/files/tex/c6ea64f1a922811340290ca2a1f8671b6181b9fb.png) możemy przyporządkować dzielnik z przedziału
możemy przyporządkować dzielnik z przedziału ![$ [2,\sqrt{n}] $](/files/tex/816f06606ef26bbc267340fe979e97b86742b6d8.png) taki, że ich iloczyn wyniesie n. Poprawmy więc nasz algorytm:
taki, że ich iloczyn wyniesie n. Poprawmy więc nasz algorytm: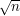 razy, w każdej stałą liczbę operacji. Przyspieszyliśmy zatem do
razy, w każdej stałą liczbę operacji. Przyspieszyliśmy zatem do 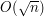 . Na pojedyńcze sprawdzenie może wystarczy.
. Na pojedyńcze sprawdzenie może wystarczy.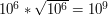 . To za wolne.
. To za wolne.
![$ [2,n] $](/files/tex/509a6ac836c01497f069c684099def0d4e8e57df.png) sprawdzić, czy są pierwsze. Nazywa się to Sitem Eratostenesa. Dla każdej liczby pierwszej wykreślmy jej wielokrotności z listy - nie bądą one przecież pierwsze.
sprawdzić, czy są pierwsze. Nazywa się to Sitem Eratostenesa. Dla każdej liczby pierwszej wykreślmy jej wielokrotności z listy - nie bądą one przecież pierwsze.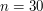 .
.
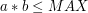 pozostanie nieoznaczona przez nasz algorytm. Skoro
pozostanie nieoznaczona przez nasz algorytm. Skoro 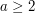 to
to 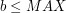 .
. 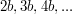 oznaczyliśmy jako złożone, co prowadzi do sprzeczności a więc wszystkie liczby złożone faktycznie oznaczyliśmy jako złożone.
oznaczyliśmy jako złożone, co prowadzi do sprzeczności a więc wszystkie liczby złożone faktycznie oznaczyliśmy jako złożone.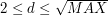 wykona
wykona 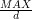 operacji. W sumie będzie to
operacji. W sumie będzie to 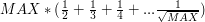 . Niech
. Niech 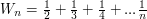 . Spróbujmy oszacować
. Spróbujmy oszacować 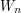 . Pogrupujmy wyrazy tak, żeby pierwszy (największy) wyraz w grupie wynosił
. Pogrupujmy wyrazy tak, żeby pierwszy (największy) wyraz w grupie wynosił 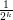 dla kolejnych
dla kolejnych 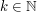 . Grup będzie
. Grup będzie 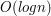 .
. 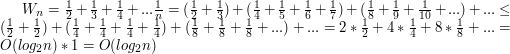
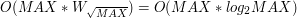 . Jest to szybkość wystarczająca.
. Jest to szybkość wystarczająca.

