Sito Eratostenesa
27.11.2009 - Anna Piekarska
 Dalsze optymalizacjeMamy szybki algorytm. Czy może on być szybszy? Nasze spostrzeżenie, że aktualnie przetwarzana liczba będzie największym dzielnikiem pierwszym skreślanej liczby przyda się raz jeszcze. Jeśli przetwarzana przez nas liczba pierwsza jest większa od
const int MAX = 1000010; // tyle liczb chcemy sprawdzić
bool p[MAX]; // tablica, w której zaznaczamy, czy liczba jest pierwsza
void init()
{
for(int i = 2; i < MAX; i++) p[i] = 1;
// na początku wszystkie liczby są pierwsze
for(int i = 2; i*i < MAX; i++)
{
if(p[i])
{
for(int j = i; i * j < MAX; j++) p[i*j] = 0;
// i*j jest wielokrotnością i, więc jest liczbą złożoną
}
}
}
bool isPrime(int n)
{
if(n < MAX) return p[n];
else cout << "Nie wiem. Liczba jest za duza" << endl;
}
A co z czynnikami pierwszymi?Znowu istnieje algorytm naiwny - sprawdzić wszystkie liczby do pierwiastka. Ale niewiele modyfikując nasz końcowy algorytm możemy szybko otrzymać rozkład liczby na czynniki pierwsze.
Coś jeszcze szybszegoIstnieją szybsze algorytmy sprawdzania pierwszości. Polegają one na randomizacji (zgadywaniu) i nie zawsze muszą dać poprawny wynik (choć w praktyce najczęściej dają). Najpopularniejsze to test Fermata oraz test Millera-Rabina. Wykorzystują właściwości szczególne tylko dla liczb pierwszych. Na przykład test Millera-Rabina wykorzystuje Małe Twierdzenie Fermata czyli Po co nam liczby pierwsze?Liczby pierwsze mają wiele właściwości, których nie mają liczby złożone. Choćby wspomniane wyżej MTF. Dzięki temu są używane na przykład w kryptografii. Umiejętność szybkiej faktoryzacji liczby staje się ważną kwestią - większość systemów szyfrujących zakłada brak efektywnego algorytmu. W przeciwnym przypadku nasze hasła oraz wiele ważnych zabezpieczeń byłoby zagrożonych. Zadanie z OlimpiadyDo tego zadania dam tylko kilka wskazówek. Po pierwsze znajdźmy liczby pierwsze do miliona oraz wykluczmy je z naszych liczb (podzielmy przez nie). Zauważmy, że liczby, które pozostały są iloczynem conajwyżej dwóch liczb pierwszych. Następnie znajdźmy wspólne dzielniki każdej pary danych liczb i je również wykluczmy. Wreszcie nie interesuje nas jakie są czynniki każdej z liczb. Chcemy tylko wiedzieć czy są 2 czy 1 czynnik pierwszy. Skorzystajmy zatem z któregoś z testów pierwszości. W następnej części artykułu znajdują się treści zadań programistycznych - zachęcam do wysłania rozwiązania. Pod każdym zadaniem znajduje się okienko do zgłaszania rozwiązań. (9 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


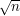 (gdzie n jest skreślaną liczbą) to na pewno była już inna liczba, której wielokrotnością było
(gdzie n jest skreślaną liczbą) to na pewno była już inna liczba, której wielokrotnością było  . W takim razie polowanie na liczby złożone możemy rozpocząć od
. W takim razie polowanie na liczby złożone możemy rozpocząć od 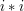 nie pomijając niczego. Prowadzi to do takiego kodu:
nie pomijając niczego. Prowadzi to do takiego kodu: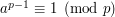 - sprawdza dla wielu liczb, czy ta kongruencja faktycznie zachodzi. Jak do tej pory istnieje jeden wielomianowy algorytm testowania pierwszości- algorytm AKS. Odkryty został w 2002 roku. Zainteresowanych odsyłam w bezdenne czeluści internetu.
- sprawdza dla wielu liczb, czy ta kongruencja faktycznie zachodzi. Jak do tej pory istnieje jeden wielomianowy algorytm testowania pierwszości- algorytm AKS. Odkryty został w 2002 roku. Zainteresowanych odsyłam w bezdenne czeluści internetu.

