Własny silnik graficzny. Część II: detekcja kolizji.
30.11.2010 - Robert Kraus
    Reprezentacja sceny Scena zawiera ona zbiót sfer, zbiór trójkątów, kamerę oraz źródło światła. W konstruktorze wczytujemy tekstury, tworzymy przy ich pomocy materiały z teksturami, a następnie tworzymy obiekty sceny (sfery i trójkąty).
Szukanie najbliższego najbliższego przecięcia
Szukamy najbliższej sfery, w którą uderza promień, wywołując procedurę
Mając najbliższy trójkąt i najbliższą sferę porównujemy ich odległości od źródła promienia i wybieramy obiekt z mniejszą odległością.
Optymalizacja Nietrudno się domyślić, że jeśli śledząc każdy promień będziemy wykonywali test przecięcia z wszystkimi obiektami sceny w celu znalezienia obiektu, z którym zderzy się promień, to będzie to mówiąc wprost lekka przesada. Można to zrobić lepiej, np. poprzez zorganizowanie zbioru obiektów w pewną strukturę danych. Jest to bardzo ważne, gdyż szacuje się, że od 80% do 90% czasu działania proramu śledzącego promienie zajmuje własnie testowanie kolizji. Jest wiele struktur danych przeznaczonych do przyspieszania śledzenia promieni, my zajmiemy się jedną z nich, będzie to kd-drzewo (ang. kd-tree) powszechnie uważaną za jedną z najlepszych. Struktura ta ma dość prostą definicję: każdy węzeł wewnętrzny drzewa reprezentuje płaszczyznę podziału sceny (która do każdej z osi układu jest równoległa lub prostopadła), natomiast w liściach drzewa znajduję się elementy sceny. Przyjrzyjmy się 2-wymiarowej wersji takiego drzewa.
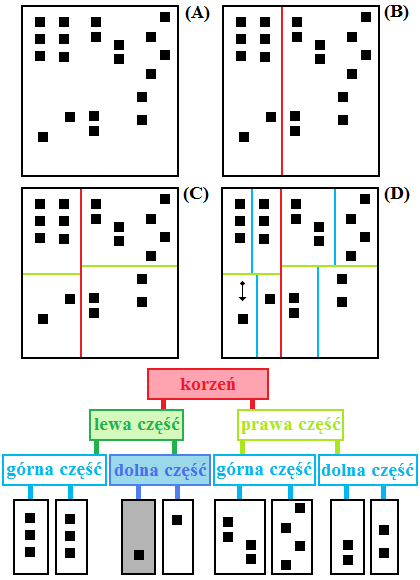
Wyobraźmy sobie, że na powyższym rysunku każdy kwadrat oznacza pewien obiekt.
Rysunek (A) przedsawia scenę zawierającą 20 obiektów bez podziału.
Śledząc promień musielibyśmy wykonać test przecięcia dla wszystkich 20 obiektów.
Na rysunku (B) dzielimy przestrzeń na dwie części pionową prostą,
na rysunku (C) dzielimy każdą z tych dwóch części jeszcze raz poziomymi odcinkami, itd.
Na rysunku (D) mamy ostatecznie podział prostymi na 3 poziomach oraz promień
o pewnym położeniu i kierunku ruchu. Widzimy dokładnie, w który kwadrat trafi nasz promień.
Komputer nie jest tak bystry, musimy mu jakoś pomóc.
Pod rysunkiem (D) znajduje się wizualizacja kd-drzewa odpowiadającego podziałowi z rysunku (D).
Zakolorowane węzły są tymi które odwiedziliśmy szukając najbliższego obiektu.
Podsumowując zamiast testowania przęcięcia z wszystkimi dwudziestoma obiektami
wykonaliśmy trzy decyzje odnośnie kierunku przechodzenia drzewa i tylko jeden test przecięcia z obiektem.
To jeszcze nie robi wrażenia, ale wyobraźmy sobie, że nasza scena zawiera Część I Część II Część III Część IV (2 ocen) |
Copyright © 2008-2010 Wrocławski Portal Informatyczny
design: rafalpolito.com


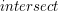 dla wszystkich sfer w scenie i wybieramy tą, dla której wynik procedury
dla wszystkich sfer w scenie i wybieramy tą, dla której wynik procedury 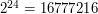 obiektów.
Przy dobrze zbudowanym kd-drzewie możemy liczbę przecięć zredukować z
obiektów.
Przy dobrze zbudowanym kd-drzewie możemy liczbę przecięć zredukować z 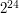 do zaledwie kilku plus około 24 decycje o kierunku przechodzenia w drzewie,
to już jest coś! Teraz czas na złe wieści, niestety budowanie tak dobrego kd-drzewa nie jest zadaniem banalnym.
Program, który do tej pory napisaliśmy zawiera małą scenę, więc takie kd-drzewo nie jest mu potrzebne.
W przyszłości rozbudujemy scenę i wtedy dowiemy się jak zbudować taką strukturę danych.
do zaledwie kilku plus około 24 decycje o kierunku przechodzenia w drzewie,
to już jest coś! Teraz czas na złe wieści, niestety budowanie tak dobrego kd-drzewa nie jest zadaniem banalnym.
Program, który do tej pory napisaliśmy zawiera małą scenę, więc takie kd-drzewo nie jest mu potrzebne.
W przyszłości rozbudujemy scenę i wtedy dowiemy się jak zbudować taką strukturę danych.


